1.任务
学习Gradient Descent、Mini-Batch Gradient descent、Momentum、Adam(RMSprop和Momentum的结合)
2.准备工作
- 导入依赖包
import numpy as np
import matplotlib.pyplot as plt
import scipy.io
import math
import sklearn
import sklearn.datasets
from opt_utils import load_params_and_grads, initialize_parameters, forward_propagation, backward_propagation
from opt_utils import compute_cost, predict, predict_dec, plot_decision_boundary, load_dataset
from testCases import *
3.四种算法介绍
3.1Gradient Descent
Gradient Descent是机器学习中一个简单的优化算法,简称GD。当对每个步骤上的所有 $m$ 示例采取梯度步骤时,它也称为批量梯度下降。
- 热身训练
实现梯度下降更新规则。梯度下降规则是,对于 $l = 1, …, L$: 来说
\(W^{[l]} = W^{[l]} - \alpha \text{ } dW^{[l]} \tag{1}\)
\(b^{[l]} = b^{[l]} - \alpha \text{ } db^{[l]} \tag{2}\)
在这段话中,“L”表示层数,“$\alpha$”表示学习率。所有参数应该存储在parameters字典中。注意迭代器l在for循环中从0开始,而第一个参数是$W^{[1]}$和$b^{[1]}$。编码时需要将l转换为l+1。
下面我们实现这个算法:
# GRADED FUNCTION: 使用梯度下降更新参数的函数
def update_parameters_with_gd(parameters, grads, learning_rate):
"""
使用梯度下降的一步来更新参数
参数:
parameters -- 包含要更新的参数的python字典:
parameters['W' + str(l)] = Wl
parameters['b' + str(l)] = bl
grads -- 包含用于更新每个参数的梯度的python字典:
grads['dW' + str(l)] = dWl
grads['db' + str(l)] = dbl
learning_rate -- 学习率,标量。
返回:
parameters -- 包含更新后参数的python字典
"""
L = len(parameters) // 2 # 神经网络中的层数
# 每个参数的更新规则
for i in range(L):
### 开始编写代码 ### (大约 2 行)
parameters["W" + str(i + 1)] -= learning_rate * grads["dW" + str(i + 1)]
parameters["b" + str(i + 1)] -= learning_rate * grads["db" + str(i + 1)]
### 结束编写代码 ###
return parameters
- 部署这段代码:
#获取测试数据
parameters, grads, learning_rate = update_parameters_with_gd_test_case()
#运行算法
parameters = update_parameters_with_gd(parameters, grads, learning_rate)
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
- 输出
W1 = [[ 1.63535156, -0.62320365, -0.53718766],
[-1.07799357, 0.85639907, -2.29470142]]
b1 = [[ 1.74604067],
[-0.75184921]]
W2 = [[ 0.32171798, -0.25467393, 1.46902454],
[-2.05617317, -0.31554548, -0.3756023 ],
[ 1.1404819, -1.09976462, -0.1612551 ]]
b2 = [[-0.88020257],
[ 0.02561572],
[ 0.57539477]]
这里有一种变体叫做随机梯度下降(SGD),它等同于小批量梯度下降,但每个小批量仅包含一个样本。我刚刚实现的更新规则并不会改变。改变的是,我将一次只对一个训练样本计算梯度,而不是对整个训练集计算。下面的代码示例展示了随机梯度下降和(批量)梯度下降之间的区别。
###(Batch) Gradient Descent:###
X = data_input
Y = labels
parameters = initialize_parameters(layers_dims)
for i in range(0, num_iterations):
# Forward propagation
a, caches = forward_propagation(X, parameters)
# Compute cost.
cost = compute_cost(a, Y)
# Backward propagation.
grads = backward_propagation(a, caches, parameters)
# Update parameters.
parameters = update_parameters(parameters, grads)
###Stochastic Gradient Descent:###
X = data_input
Y = labels
parameters = initialize_parameters(layers_dims)
for i in range(0, num_iterations):
for j in range(0, m):
# Forward propagation
a, caches = forward_propagation(X[:,j], parameters)
# Compute cost
cost = compute_cost(a, Y[:,j])
# Backward propagation
grads = backward_propagation(a, caches, parameters)
# Update parameters.
parameters = update_parameters(parameters, grads)
在随机梯度下降中,更新梯度之前只使用一个训练样本。当训练集很大时,随机梯度下降可以更快。但是,参数会向最小值“振荡”,而不是平滑地收敛。这里有一个这种情况的示意图:
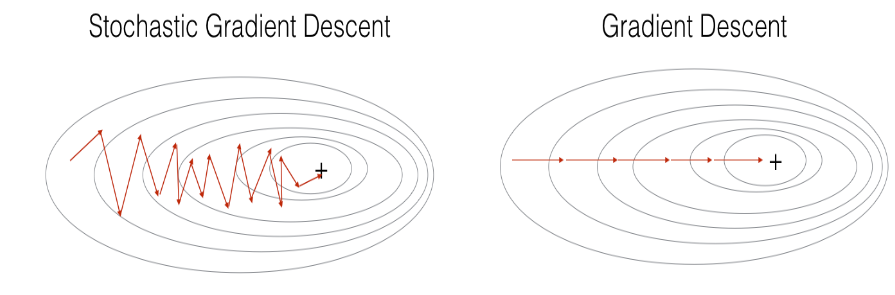
在实际应用中,如果既不使用整个训练集,也不仅使用一个训练样本来进行每次更新,通常会得到更快的结果。Mini-Batch Gradient descent使用中间数量的样本来进行每一步的更新。使用Mini-Batch Gradient descent时,训练时会遍历小批量样本而不是单个训练样本。
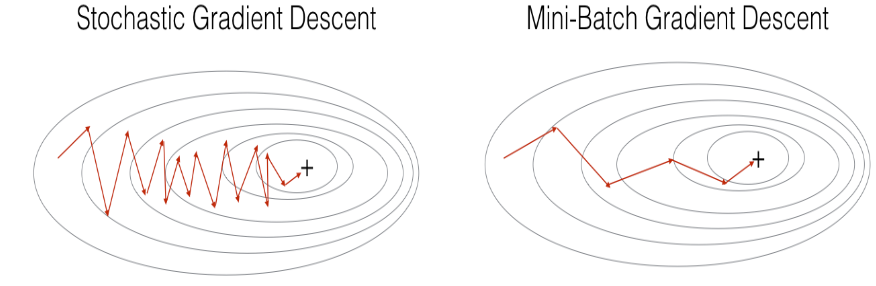
我们应该额外关注的是:
- 梯度下降、小批量梯度下降和随机梯度下降之间的区别在于你用来进行一次更新步骤的样本数量。
- 你需要调整学习率超参数$\alpha$。
- 使用一个调整得当的小批量大小,通常它会优于梯度下降或随机梯度下降(特别是当训练集很大时)
3.2Mini-Batch Gradient descent
该算法主要分为两步:
- Shuffle(洗牌)
如下所示,创建一个训练集(X, Y)的打乱版本。X和Y的每一列代表一个训练样本。注意,X和Y之间的随机洗牌是同步进行的。这样在洗牌后,X的第$i^{th}$列是与Y中第$i^{th}$标签对应的样本。洗牌步骤确保样本将随机分配到不同的小批量中。
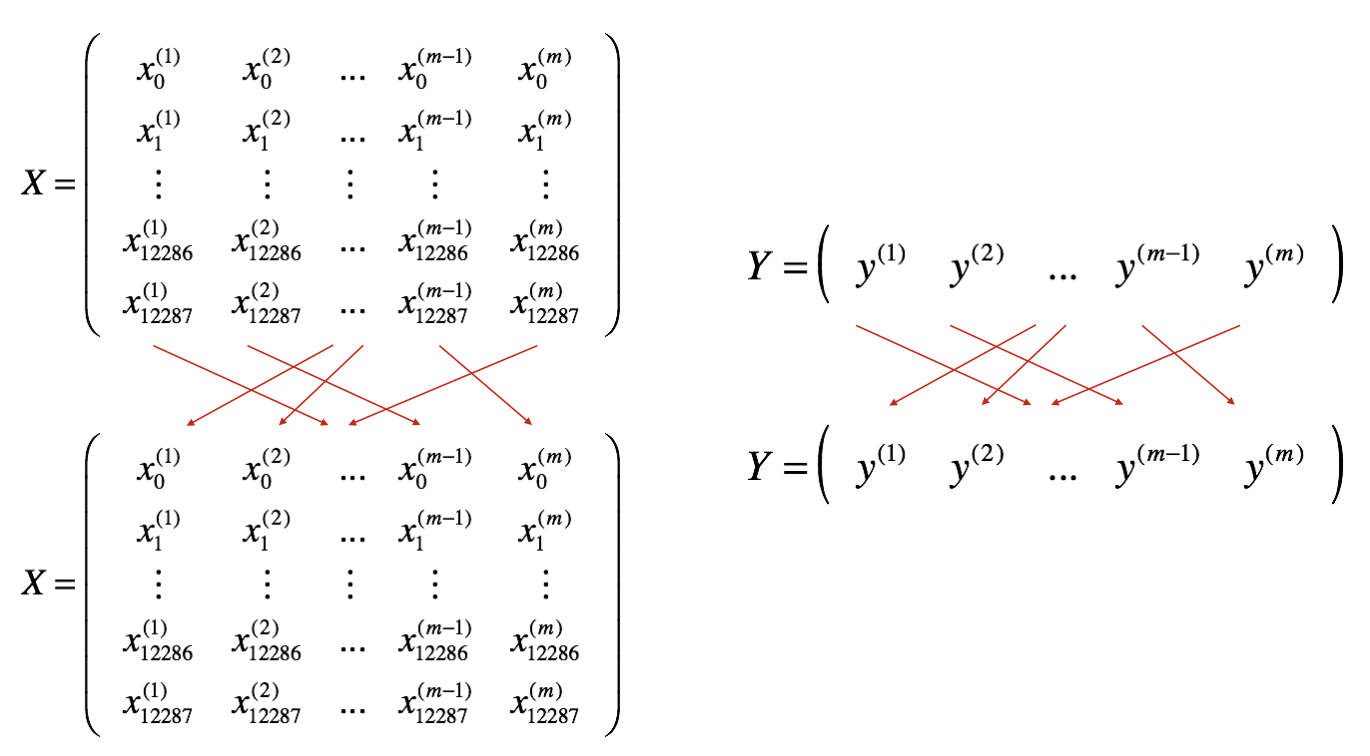
- Partition(分割)
将打乱的(X, Y)分割成大小为mini_batch_size(这里是64)的小批量。注意,训练样本的数量并不总是能被mini_batch_size整除。最后一个小批量可能会更小,但这不需要担心。当最终的小批量小于完整的mini_batch_size时,它将如下所示:
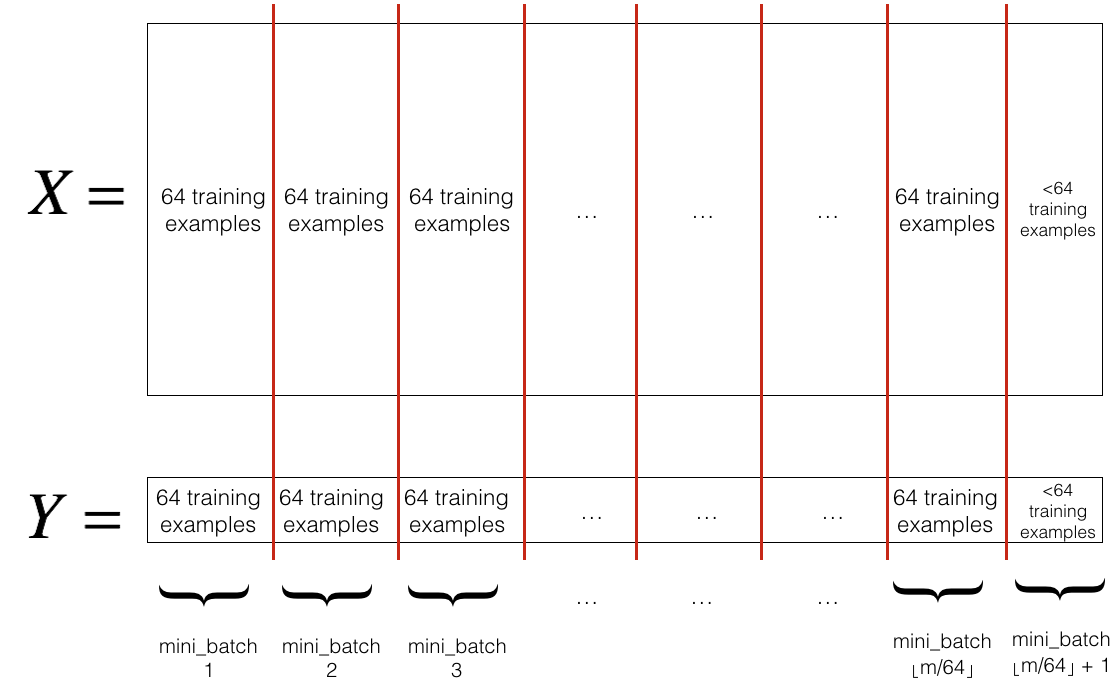
下面我们实现这个算法:
# GRADED FUNCTION: 随机生成小批量的函数
def random_mini_batches(X, Y, mini_batch_size = 64, seed = 0):
"""
从 (X, Y) 中创建随机小批量的列表
参数:
X -- 输入数据,形状为 (输入大小, 样本数量)
Y -- 真实的“标签”向量(蓝点为1 / 红点为0),形状为 (1, 样本数量)
mini_batch_size -- 小批量的大小,整数
返回:
mini_batches -- 同步的 (mini_batch_X, mini_batch_Y) 列表
"""
np.random.seed(seed) # 为了使你的“随机”小批量与我们的相同
m = X.shape[1] # 训练样本的数量
mini_batches = []
# 第一步:洗牌 (X, Y)
permutation = list(np.random.permutation(m))
shuffled_X = X[:, permutation]
shuffled_Y = Y[:, permutation].reshape((1,m))
# 第二步:分割 (shuffled_X, shuffled_Y),排除最后一个案例。
num_complete_minibatches = math.floor(m/mini_batch_size) # 在你的分割中,大小为 mini_batch_size 的小批量的数量
for k in range(0, num_complete_minibatches):
### 开始编码 ### (大约 2 行)
mini_batch_X = shuffled_X[:, k * mini_batch_size : (k + 1) * mini_batch_size]
mini_batch_Y = shuffled_Y[:, k * mini_batch_size : (k + 1) * mini_batch_size]
### 结束编码 ###
mini_batch = (mini_batch_X, mini_batch_Y)
mini_batches.append(mini_batch)
# 处理最后一个案例(最后一个小批量 < mini_batch_size)
if m % mini_batch_size != 0:
### 开始编码 ### (大约 2 行)
mini_batch_X = shuffled_X[:, num_complete_minibatches * mini_batch_size : m]
mini_batch_Y = shuffled_Y[:, num_complete_minibatches * mini_batch_size : m]
### 结束编码 ###
mini_batch = (mini_batch_X, mini_batch_Y)
mini_batches.append(mini_batch)
return mini_batches
- 部署代码:
X_assess, Y_assess, mini_batch_size = random_mini_batches_test_case()
mini_batches = random_mini_batches(X_assess, Y_assess, mini_batch_size)
print ("shape of the 1st mini_batch_X: " + str(mini_batches[0][0].shape))
print ("shape of the 2nd mini_batch_X: " + str(mini_batches[1][0].shape))
print ("shape of the 3rd mini_batch_X: " + str(mini_batches[2][0].shape))
print ("shape of the 1st mini_batch_Y: " + str(mini_batches[0][1].shape))
print ("shape of the 2nd mini_batch_Y: " + str(mini_batches[1][1].shape))
print ("shape of the 3rd mini_batch_Y: " + str(mini_batches[2][1].shape))
print ("mini batch sanity check: " + str(mini_batches[0][0][0][0:3]))
- 输出:
shape of the 1st mini_batch_X: (12288, 64)
shape of the 2nd mini_batch_X: (12288, 64)
shape of the 3rd mini_batch_X: (12288, 20)
shape of the 1st mini_batch_Y: (1, 64)
shape of the 2nd mini_batch_Y: (1, 64)
shape of the 3rd mini_batch_Y: (1, 20)
mini batch sanity check: [ 0.90085595 -0.7612069 0.2344157 ]
3.3Momentum
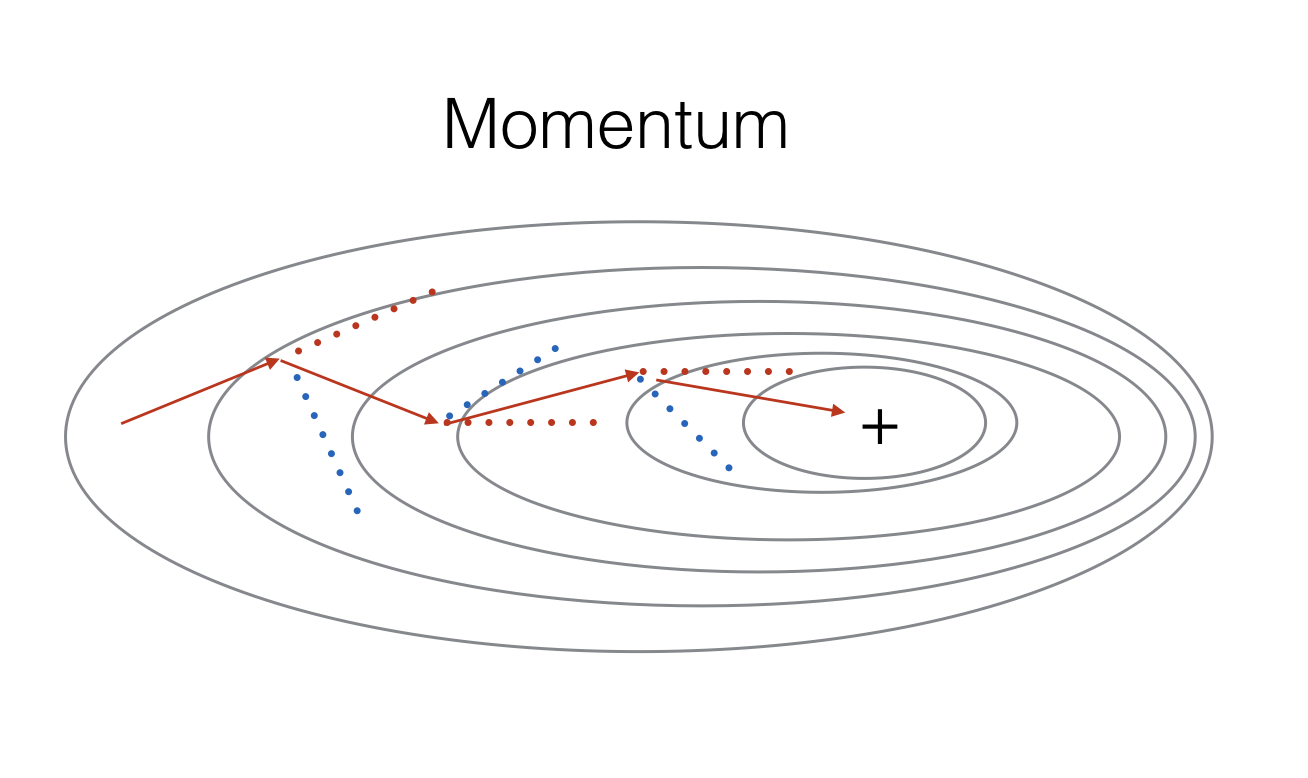
由于Mini-Batch Gradient descent在仅看到示例子集后进行参数更新,因此更新的方向存在一定方差,因此Mini-Batch Gradient descent所采取的路径将“振荡”收敛。 利用Momentum可以减少这些振荡。
Momentum考虑了过去的梯度来平滑更新。 我们将先前梯度的“方向”存储在变量 $v$ 中。 形式上,这将是先前步骤梯度的指数加权平均值。 您还可以将 $v$ 视为滚下山的球的“速度”,根据山坡的梯度/坡度方向增加速度(和动量)。
下面我们实现这个算法:
首先是初始化速度
# GRADED FUNCTION: 初始化速度
def initialize_velocity(parameters):
"""
以python字典的形式初始化速度,其中:
- 键: "dW1", "db1", ..., "dWL", "dbL"
- 值:与相应梯度/参数形状相同的零值numpy数组。
参数:
parameters -- 包含你的参数的python字典。
parameters['W' + str(l)] = Wl
parameters['b' + str(l)] = bl
返回:
v -- 包含当前速度的python字典。
v['dW' + str(l)] = dWl的速度
v['db' + str(l)] = dbl的速度
"""
L = len(parameters) // 2 # 神经网络中的层数
v = {}
# 初始化速度
for i in range(L):
### 开始编码 ### (大约 2 行)
v['dW' + str(i + 1)] = np.zeros(parameters["W" + str(i + 1)].shape)
v['db' + str(i + 1)] = np.zeros(parameters["b" + str(i + 1)].shape)
### 结束编码 ###
return v
- 部署代码:
parameters = initialize_velocity_test_case()
v = initialize_velocity(parameters)
print("v[\"dW1\"] = " + str(v["dW1"]))
print("v[\"db1\"] = " + str(v["db1"]))
print("v[\"dW2\"] = " + str(v["dW2"]))
print("v[\"db2\"] = " + str(v["db2"]))
- 输出:
v["dW1"] = [[0.0, 0.0, 0.0],
[0.0, 0.0, 0.0]]
v["db1"] = [[0.0],
[0.0]]
v["dW2"] = [[0.0, 0.0, 0.0],
[0.0, 0.0, 0.0],
[0.0, 0.0, 0.0]]
v["db2"] = [[0.0],
[0.0],
[0.0]]
接着是momentum算法实现参数的更新。动量更新规则是,对于 $l = 1, …, L$:
\(\begin{cases} v_{dW^{[l]}} = \beta v_{dW^{[l]}} + (1 - \beta) dW^{[l]} \\ W^{[l]} = W^{[l]} - \alpha v_{dW^{[l]}} \end{cases}\tag{3}\)
\(\begin{cases} v_{db^{[l]}} = \beta v_{db^{[l]}} + (1 - \beta) db^{[l]} \\ b^{[l]} = b^{[l]} - \alpha v_{db^{[l]}} \end{cases}\tag{4}\)
其中L是层数,$\beta$ 是动量,$\alpha$ 是学习率。所有参数应该存储在parameters字典中。注意迭代器l在for循环中从0开始,而第一个参数是 $W^{[1]}$ 和 $b^{[1]}$(这里的上标是“一”)。因此,在编码时需要将l改为l+1。
# GRADED FUNCTION: 使用动量更新参数的函数
def update_parameters_with_momentum(parameters, grads, v, beta, learning_rate):
"""
使用动量方法更新参数
参数:
parameters -- 包含你的参数的python字典:
parameters['W' + str(l)] = Wl
parameters['b' + str(l)] = bl
grads -- 包含每个参数梯度的python字典:
grads['dW' + str(l)] = dWl
grads['db' + str(l)] = dbl
v -- 包含当前速度的python字典:
v['dW' + str(l)] = ...
v['db' + str(l)] = ...
beta -- 动量超参数,标量
learning_rate -- 学习率,标量
返回:
parameters -- 包含更新后参数的python字典
v -- 包含更新后速度的python字典
"""
L = len(parameters) // 2 # 神经网络中的层数
# 每个参数的动量更新
for i in range(L):
### 开始编码 ### (大约 4 行)
# 计算速度
v['dW' + str(i + 1)] = beta * v['dW' + str(i + 1)] + (1 - beta) * grads['dW' + str(i + 1)]
v['db' + str(i + 1)] = beta * v['db' + str(i + 1)] + (1 - beta) * grads['db' + str(i + 1)]
# 更新参数
parameters['W' + str(i + 1)] -= learning_rate * v['dW' + str(i + 1)]
parameters['b' + str(i + 1)] -= learning_rate * v['db' + str(i + 1)]
### 结束编码 ###
return parameters, v
- 部署算法
parameters, grads, v = update_parameters_with_momentum_test_case()
parameters, v = update_parameters_with_momentum(parameters, grads, v, beta = 0.9, learning_rate = 0.01)
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
print("v[\"dW1\"] = " + str(v["dW1"]))
print("v[\"db1\"] = " + str(v["db1"]))
print("v[\"dW2\"] = " + str(v["dW2"]))
print("v[\"db2\"] = " + str(v["db2"]))
- 输出
W1 = [[ 1.62544598, -0.61290114, -0.52907334],
[-1.07347112, 0.86450677, -2.30085497]]
b1 = [[ 1.74493465],
[-0.76027113]]
W2 = [[ 0.31930698, -0.24990073, 1.4627996 ],
[-2.05974396, -0.32173003, -0.38320915],
[ 1.13444069, -1.0998786, -0.1713109 ]]
b2 = [[-0.87809283],
[ 0.04055394],
[ 0.58207317]]
v["dW1"] = [[-0.11006192, 0.11447237, 0.09015907],
[ 0.05024943, 0.09008559, -0.06837279]]
v["db1"] = [[-0.01228902],
[-0.09357694]]
v["dW2"] = [[-0.02678881, 0.05303555, -0.06916608],
[-0.03967535, -0.06871727, -0.08452056],
[-0.06712461, -0.00126646, -0.11173103]]
v["db2"] = [[ 0.02344157],
[ 0.16598022],
[ 0.07420442]]
**这个算法需要额外注意的是**:
- 速度是以0开始初始化的。因此,算法需要几次迭代来“积累”速度并开始采取更大的步伐。
- 如果 $\beta = 0$,那么这就变成了没有动量的标准梯度下降。
**如何选择$\beta$?**
- 动量 $\beta$ 越大,更新就越平滑,因为我们考虑了更多过去的梯度。但是,如果 $\beta$ 太大,也可能过度平滑更新。
- $\beta$ 的常见值范围从 0.8 到 0.999。如果你不想调整这个值,$\beta = 0.9$ 通常是一个合理的默认选择。
- 为你的模型调整最优的 $\beta$ 可能需要尝试多个值,以查看哪个在降低成本函数 $J$ 的值方面效果最好。
3.4Adam
- 工作机制
- 它计算过去梯度的指数加权平均值,并将其存储在变量 $v$(未进行偏差校正前)和 $v^{corrected}$(进行偏差校正后)中。
- 它计算过去梯度平方的指数加权平均值,并将其存储在变量 $s$(未进行偏差校正前)和 $s^{corrected}$(进行偏差校正后)中。
- 它基于结合“1”和“2”的信息来更新参数。
更新规则,对于 $l = 1, …, L$:
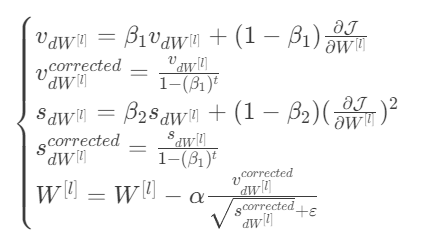
其中:
- t 表示 Adam 执行的步数
- L 是层数
- $\beta_1$ 和 $\beta_2$ 是控制两个指数加权平均的超参数。
- $\alpha$ 是学习率
- $\varepsilon$ 是一个非常小的数,用来避免除以零 像往常一样,我们会将所有参数存储在
parameters字典中。
下面我们实现这个算法:
首先是初始化
# GRADED FUNCTION: 初始化Adam算法的函数
def initialize_adam(parameters) :
"""
以两个python字典的形式初始化 v 和 s:
- 键: "dW1", "db1", ..., "dWL", "dbL"
- 值:形状与相应梯度/参数相同的零值numpy数组。
参数:
parameters -- 包含你的参数的python字典。
parameters["W" + str(l)] = Wl
parameters["b" + str(l)] = bl
返回:
v -- 将包含梯度指数加权平均的python字典。
v["dW" + str(l)] = ...
v["db" + str(l)] = ...
s -- 将包含平方梯度指数加权平均的python字典。
s["dW" + str(l)] = ...
s["db" + str(l)] = ...
"""
L = len(parameters) // 2 # 神经网络中的层数
v = {}
s = {}
# 初始化 v, s。输入:"parameters"。输出:"v, s"。
for i in range(L):
### 开始编码 ### (大约 4 行)
v["dW" + str(i + 1)] = np.zeros(parameters["W" + str(i + 1)].shape)
v["db" + str(i + 1)] = np.zeros(parameters["b" + str(i + 1)].shape)
s["dW" + str(i + 1)] = np.zeros(parameters["W" + str(i + 1)].shape)
s["db" + str(i + 1)] = np.zeros(parameters["b" + str(i + 1)].shape)
### 结束编码 ###
return v, s
- 部署代码
parameters = initialize_adam_test_case()
v, s = initialize_adam(parameters)
print("v[\"dW1\"] = " + str(v["dW1"]))
print("v[\"db1\"] = " + str(v["db1"]))
print("v[\"dW2\"] = " + str(v["dW2"]))
print("v[\"db2\"] = " + str(v["db2"]))
print("s[\"dW1\"] = " + str(s["dW1"]))
print("s[\"db1\"] = " + str(s["db1"]))
print("s[\"dW2\"] = " + str(s["dW2"]))
print("s[\"db2\"] = " + str(s["db2"]))
- 输出
v["dW1"] = [[0.0, 0.0, 0.0],
[0.0, 0.0, 0.0]]
v["db1"] = [[0.0],
[0.0]]
v["dW2"] = [[0.0, 0.0, 0.0],
[0.0, 0.0, 0.0],
[0.0, 0.0, 0.0]]
v["db2"] = [[0.0],
[0.0],
[0.0]]
s["dW1"] = [[0.0, 0.0, 0.0],
[0.0, 0.0, 0.0]]
s["db1"] = [[0.0],
[0.0]]
s["dW2"] = [[0.0, 0.0, 0.0],
[0.0, 0.0, 0.0],
[0.0, 0.0, 0.0]]
s["db2"] = [[0.0],
[0.0],
[0.0]]
接着我们利用写好的初始化函数和上述提到的Adam算法公式来写出对应的函数:
# GRADED FUNCTION: 使用Adam更新参数的函数
def update_parameters_with_adam(parameters, grads, v, s, t, learning_rate = 0.01,
beta1 = 0.9, beta2 = 0.999, epsilon = 1e-8):
"""
使用Adam方法更新参数
参数:
parameters -- 包含你的参数的python字典:
parameters['W' + str(l)] = Wl
parameters['b' + str(l)] = bl
grads -- 包含每个参数梯度的python字典:
grads['dW' + str(l)] = dWl
grads['db' + str(l)] = dbl
v -- Adam变量,第一梯度的移动平均值,python字典
s -- Adam变量,平方梯度的移动平均值,python字典
learning_rate -- 学习率,标量。
beta1 -- 第一时刻估计的指数衰减超参数
beta2 -- 第二时刻估计的指数衰减超参数
epsilon -- 防止Adam更新中除以零的超参数
返回:
parameters -- 包含更新后参数的python字典
v -- Adam变量,第一梯度的移动平均值,python字典
s -- Adam变量,平方梯度的移动平均值,python字典
"""
L = len(parameters) // 2 # 神经网络中的层数
v_corrected = {} # 初始化第一时刻估计,python字典
s_corrected = {} # 初始化第二时刻估计,python字典
# 对所有参数执行Adam更新
for i in range(L):
# 计算梯度的移动平均值。输入:"v, grads, beta1"。输出:"v"。
### 开始编码 ### (大约 2 行)
v["dW" + str(i + 1)] = beta1 * v["dW" + str(i + 1)] + (1 - beta1) * grads["dW" + str(i + 1)]
v["db" + str(i + 1)] = beta1 * v["db" + str(i + 1)] + (1 - beta1) * grads["db" + str(i + 1)]
### 结束编码 ###
# 计算校正后的第一时刻估计。输入:"v, beta1, t"。输出:"v_corrected"。
### 开始编码 ### (大约 2 行)
v_corrected["dW" + str(i + 1)] = v["dW" + str(i + 1)] / (1 - beta1 ** t)
v_corrected["db" + str(i + 1)] = v["db" + str(i + 1)] / (1 - beta1 ** t)
### 结束编码 ###
# 计算平方梯度的移动平均值。输入:"s, grads, beta2"。输出:"s"。
### 开始编码 ### (大约 2 行)
s["dW" + str(i + 1)] = beta2 * s["dW" + str(i + 1)] + (1 - beta2) * np.multiply(grads["dW" + str(i + 1)], grads["dW" + str(i + 1)])
s["db" + str(i + 1)] = beta2 * s["db" + str(i + 1)] + (1 - beta2) * np.multiply(grads["db" + str(i + 1)], grads["db" + str(i + 1)])
### 结束编码 ###
# 计算校正后的第二原始时刻估计。输入:"s, beta2, t"。输出:"s_corrected"。
### 开始编码 ### (大约 2 行)
s_corrected["dW" + str(i + 1)] = s["dW" + str(i + 1)] / (1 - beta2 ** t)
s_corrected["db" + str(i + 1)] = s["db" + str(i + 1)] / (1 - beta2 ** t)
### 结束编码 ###
# 更新参数。输入:"parameters, learning_rate, v_corrected, s_corrected, epsilon"。输出:"parameters"。
### 开始编码 ### (大约 2 行)
parameters["W" + str(i + 1)] -= learning_rate * v_corrected["dW" + str(i + 1)] / (epsilon + np.sqrt(s_corrected["dW" + str(i + 1)]))
parameters["b" + str(i + 1)] -= learning_rate * v_corrected["db" + str(i + 1)] / (epsilon + np.sqrt(s_corrected["db" + str(i + 1)]))
### 结束编码 ###
return parameters, v, s
- 代码部署
parameters, grads, v, s = update_parameters_with_adam_test_case()
parameters, v, s = update_parameters_with_adam(parameters, grads, v, s, t = 2)
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
print("v[\"dW1\"] = " + str(v["dW1"]))
print("v[\"db1\"] = " + str(v["db1"]))
print("v[\"dW2\"] = " + str(v["dW2"]))
print("v[\"db2\"] = " + str(v["db2"]))
print("s[\"dW1\"] = " + str(s["dW1"]))
print("s[\"db1\"] = " + str(s["db1"]))
print("s[\"dW2\"] = " + str(s["dW2"]))
print("s[\"db2\"] = " + str(s["db2"]))
- 输出
W1 = [[ 1.63178673, -0.61919778, -0.53561312],
[-1.08040999, 0.85796626, -2.29409733]]
b1 = [[ 1.75225313],
[-0.75376553]]
W2 = [[ 0.32648046, -0.25681174, 1.46954931],
[-2.05269934, -0.31497584, -0.37661299],
[ 1.14121081, -1.09244991, -0.16498684]]
b2 = [[-0.88529979],
[ 0.03477238],
[ 0.57537385]]
v["dW1"] = [[-0.11006192, 0.11447237, 0.09015907],
[ 0.05024943, 0.09008559, -0.06837279]]
v["db1"] = [[-0.01228902],
[-0.09357694]]
v["dW2"] = [[-0.02678881, 0.05303555, -0.06916608],
[-0.03967535, -0.06871727, -0.08452056],
[-0.06712461, -0.00126646, -0.11173103]]
v["db2"] = [[ 0.02344157],
[ 0.16598022],
[ 0.07420442]]
s["dW1"] = [[0.00121136, 0.00131039, 0.00081287],
[0.0002525, 0.00081154, 0.00046748]]
s["db1"] = [[1.51020075e-05],
[8.75664434e-04]]
s["dW2"] = [[7.17640232e-05, 2.81276921e-04, 4.78394595e-04],
...
[4.50571368e-04, 1.60392066e-07, 1.24838242e-03]]
s["db2"] = [[5.49507194e-05],
[2.75494327e-03],
[5.50629536e-04]]
4四种算法在模型中的可视化对比
4.1准备工作
- 导入数据
train_X, train_Y = load_dataset()
- 定义可视化图函数用于观察三种优化函数的效果
def plot_decision_boundary(model, X, y):
#import pdb;pdb.set_trace()
# Set min and max values and give it some padding
x_min, x_max = X[0, :].min() - 1, X[0, :].max() + 1
y_min, y_max = X[1, :].min() - 1, X[1, :].max() + 1
h = 0.01
# Generate a grid of points with distance h between them
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
# Predict the function value for the whole grid
Z = model(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# Plot the contour and training examples
plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)
plt.ylabel('x2')
plt.xlabel('x1')
y = y.reshape(X[0,:].shape)#must reshape,otherwise confliction with dimensions
plt.scatter(X[0, :], X[1, :], c=y, cmap=plt.cm.Spectral)
plt.show()
4.2定义模型
我们已经实现了一个三层神经网络。你将用以下方法来训练它:
- Mini-batch Gradient Descent:它会调用你的函数:
update_parameters_with_gd()
- Mini-batchMomentum:它会调用你的函数:
initialize_velocity()和update_parameters_with_momentum()
- Mini-batch Adam:它会调用你的函数:
initialize_adam()和update_parameters_with_adam()
- 模型代码:
def model(X, Y, layers_dims, optimizer, learning_rate=0.0007, mini_batch_size=64, beta=0.9,
beta1=0.9, beta2=0.999, epsilon=1e-8, num_epochs=10000, print_cost=True):
"""
可以在不同优化器模式下运行的三层神经网络模型。
参数:
X -- 输入数据,形状为 (2, 样本数量)
Y -- 真实的“标签”向量(蓝点为1 / 红点为0),形状为 (1, 样本数量)
layers_dims -- python列表,包含每层的大小
learning_rate -- 学习率,标量。
mini_batch_size -- 小批量的大小
beta -- 动量超参数
beta1 -- 过去梯度估计的指数衰减超参数
beta2 -- 过去平方梯度估计的指数衰减超参数
epsilon -- 防止Adam更新中除以零的超参数
num_epochs -- 迭代次数
print_cost -- 如果为True,每1000次迭代打印一次成本
返回:
parameters -- 包含更新后参数的python字典
"""
L = len(layers_dims) # 神经网络中的层数
costs = [] # 用于跟踪成本
t = 0 # 初始化Adam更新所需的计数器
seed = 10 # 出于评分目的,确保你的“随机”小批量与我们的相同
# 初始化参数
parameters = initialize_parameters(layers_dims)
# 初始化优化器
if optimizer == "gd":
pass # 梯度下降不需要初始化
elif optimizer == "momentum":
v = initialize_velocity(parameters)
elif optimizer == "adam":
v, s = initialize_adam(parameters)
# 优化循环
for i in range(num_epochs):
# 定义随机小批量。每个周期后我们增加种子以不同地重洗数据集
seed = seed + 1
minibatches = random_mini_batches(X, Y, mini_batch_size, seed)
for minibatch in minibatches:
# 选择一个小批量
(minibatch_X, minibatch_Y) = minibatch
# 正向传播
a3, caches = forward_propagation(minibatch_X, parameters)
# 计算成本
cost = compute_cost(a3, minibatch_Y)
# 反向传播
grads = backward_propagation(minibatch_X, minibatch_Y, caches)
# 更新参数
if optimizer == "gd":
parameters = update_parameters_with_gd(parameters, grads, learning_rate)
elif optimizer == "momentum":
parameters, v = update_parameters_with_momentum(parameters, grads, v, beta, learning_rate)
elif optimizer == "adam":
t = t + 1 # Adam计数器
parameters, v, s = update_parameters_with_adam(parameters, grads, v, s,
t, learning_rate, beta1, beta2, epsilon)
# 每1000次迭代打印成本
if print_cost and i % 1000 == 0:
print("迭代次数 %i 后的成本: %f" % (i, cost))
if print_cost and i % 100 == 0:
costs.append(cost)
# 绘制成本图
plt.plot(costs)
plt.ylabel('成本')
plt.xlabel('迭代次数(每100次)')
plt.title("学习率 = " + str(learning_rate))
plt.show()
return parameters
4.3对比算法效果
4.3.1Mini-batch Gradient descent
# train 3-layer model
layers_dims = [train_X.shape[0], 5, 2, 1]
parameters = model(train_X, train_Y, layers_dims, optimizer = "gd")
# Predict
predictions = predict(train_X, train_Y, parameters)
# Plot decision boundary
plt.title("Model with Gradient Descent optimization")
axes = plt.gca()
axes.set_xlim([-1.5,2.5])
axes.set_ylim([-1,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)
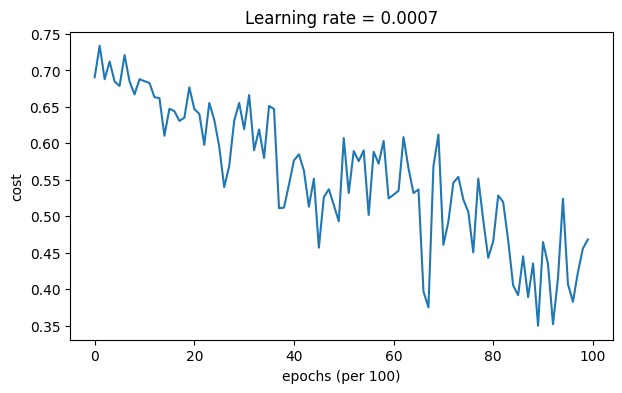
Accuracy: 0.7966666666666666
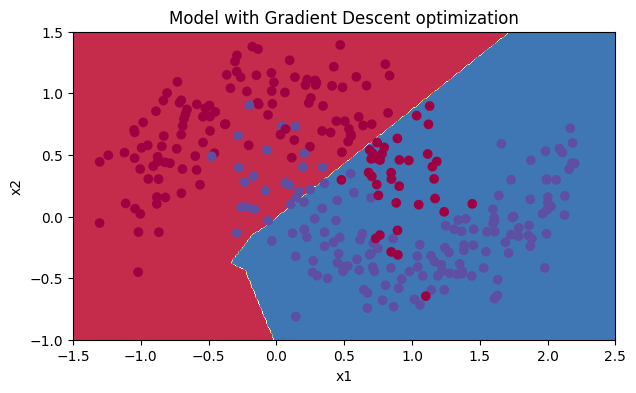
4.3.2Mini-batch gradient descent with momentum
# train 3-layer model
layers_dims = [train_X.shape[0], 5, 2, 1]
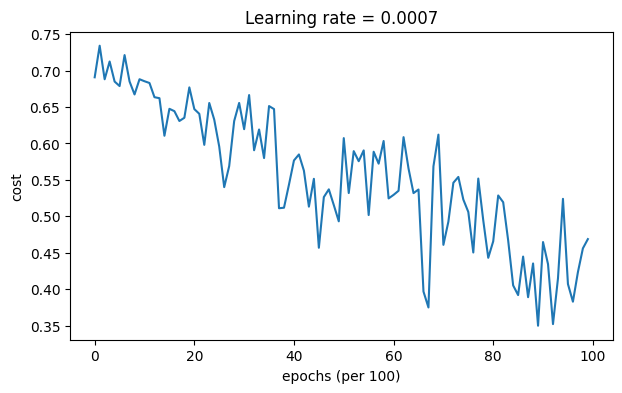
parameters = model(train_X, train_Y, layers_dims, beta = 0.9, optimizer = "momentum")
# Predict
predictions = predict(train_X, train_Y, parameters)
# Plot decision boundary
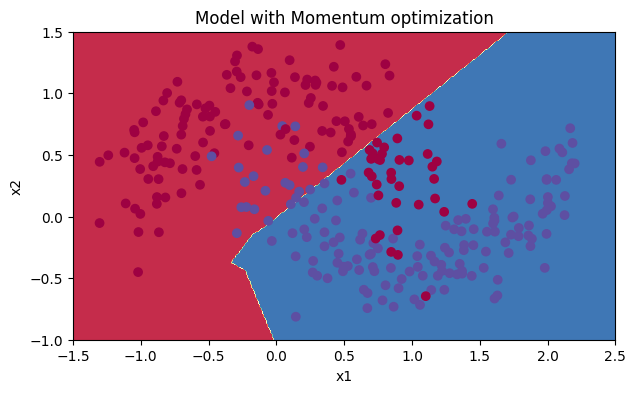
plt.title("Model with Momentum optimization")
axes = plt.gca()
axes.set_xlim([-1.5,2.5])
axes.set_ylim([-1,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)
Accuracy: 0.7966666666666666
4.3.3Mini-batch with Adam mode
# train 3-layer model
layers_dims = [train_X.shape[0], 5, 2, 1]
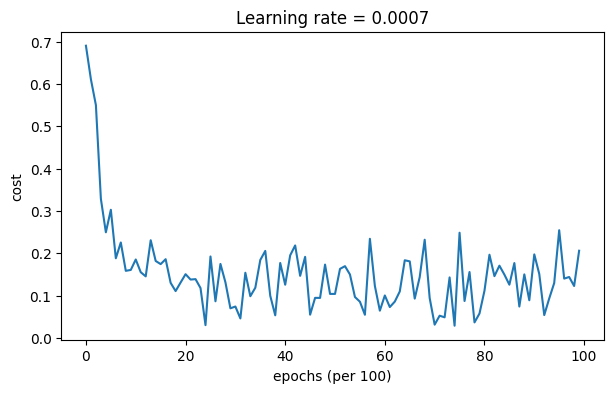
parameters = model(train_X, train_Y, layers_dims, optimizer = "adam")
# Predict
predictions = predict(train_X, train_Y, parameters)
# Plot decision boundary
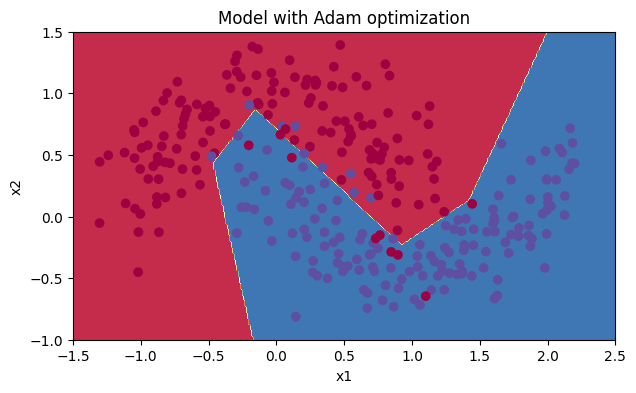
plt.title("Model with Adam optimization")
axes = plt.gca()
axes.set_xlim([-1.5,2.5])
axes.set_ylim([-1,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)
Accuracy: 0.94
5.总结
Momentum通常有所帮助,但鉴于较小的学习率和简单的数据集,其影响几乎可以忽略不计。此外,你在成本中看到的巨大波动来自于一些小批量对优化算法来说比其他批量更难处理的事实。
另一方面,Adam明显优于mini-batch gradient descent和Momentum。如果在这个简单的数据集上运行更多的迭代,所有三种方法都会导致非常好的结果。然而,你已经看到Adam收敛得更快。
Adam的一些优点包括:
- 相对较低的内存要求(尽管高于梯度下降和带动量的梯度下降)
- 通常即使在很少调整超参数的情况下也能表现良好($\alpha$ 除外)