1.任务
创建并且部署一个深度神经网络来进行监督学习
2.数据预处理
2.1导入依赖包
import time
import numpy as np
import h5py
import matplotlib.pyplot as plt
import scipy
from PIL import Image
from scipy import ndimage
from dnn_app_utils_v2 import *
import datetime
%matplotlib inline
plt.rcParams['figure.figsize'] = (5.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
%load_ext autoreload
%autoreload 2
np.random.seed(1)
2.2导入数据集
这里使用的是之前案例中的“Cat vs non-Cat”数据集”data.h5”
- 数据集介绍:
- 标记为猫(1)或非猫(0)的m_train图像的训练集
- m_test图像标记为猫和非猫的测试集
- 每个图像的形状是(num_px, num_px, 3),其中3是3通道(RGB)。
train_x_orig, train_y, test_x_orig, test_y, classes = load_data()
- 数据形状查看:
m_train = train_x_orig.shape[0]
num_px = train_x_orig.shape[1]
m_test = test_x_orig.shape[0]
print ("Number of training examples: " + str(m_train))
print ("Number of testing examples: " + str(m_test))
print ("Each image is of size: (" + str(num_px) + ", " + str(num_px) + ", 3)")
print ("train_x_orig shape: " + str(train_x_orig.shape))
print ("train_y shape: " + str(train_y.shape))
print ("test_x_orig shape: " + str(test_x_orig.shape))
print ("test_y shape: " + str(test_y.shape))
输出:
Number of training examples: 209
Number of testing examples: 50
Each image is of size: (64, 64, 3)
train_x_orig shape: (209, 64, 64, 3)
train_y shape: (1, 209)
test_x_orig shape: (50, 64, 64, 3)
test_y shape: (1, 50)
- 在把它们输入网络之前应该先归一化并reshape!
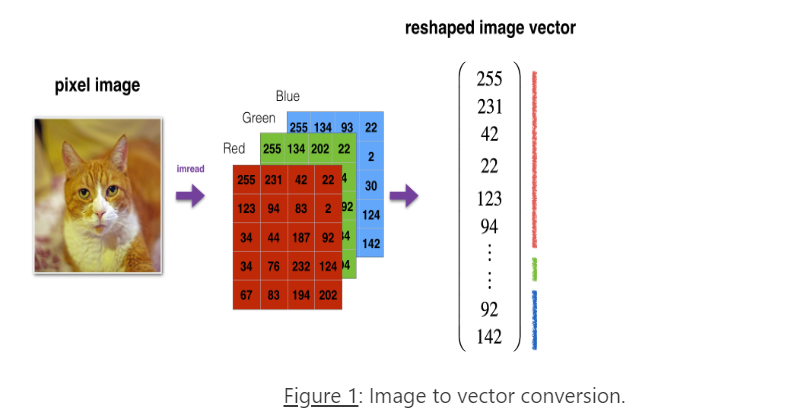
train_x_flatten = train_x_orig.reshape(train_x_orig.shape[0],-1).T
test_x_faltten = test_x_orig.reshape(test_x_orig.shape[0],-1).T
train_x = train_x_flatten/255
test_x = test_x_faltten/255
print ("train_x's shape: " + str(train_x.shape))
print ("test_x's shape: " + str(test_x.shape))
print ("train_x_orig: " + str(train_x_orig.shape))
print ("test_x_orig: " + str(test_x_orig.shape))
输出:
train_x's shape: (12288, 209) #209*64*64
test_x's shape: (12288, 50) #50*64*64
train_x_orig: (209, 64, 64, 3)
test_x_orig: (50, 64, 64, 3)
3.架构模型
架构两种模型:
- A 2-layer neural network
- An L-layer deep neural network
3.1 2-layer neural network
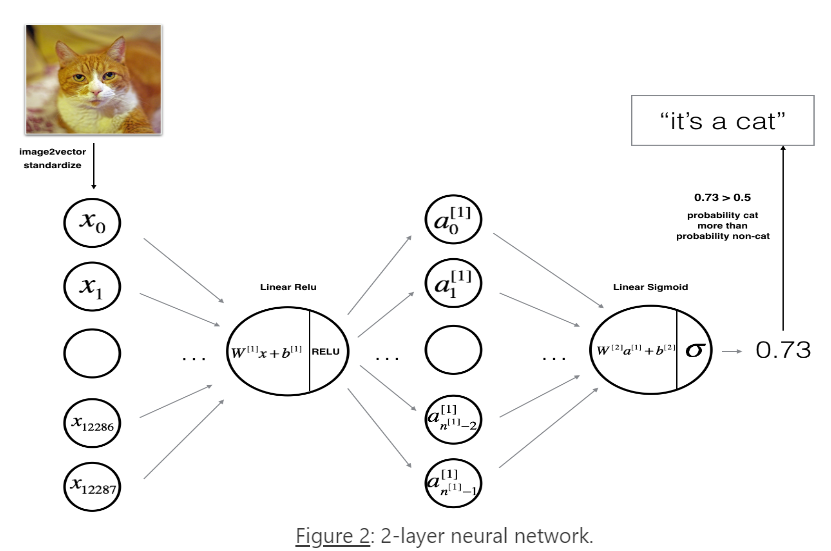
这个模型可以总结为:
INPUT -> LINEAR -> RELU -> LINEAR -> SIGMOID -> OUTPUT
具体细节介绍:

3.2 L-layer deep neural network
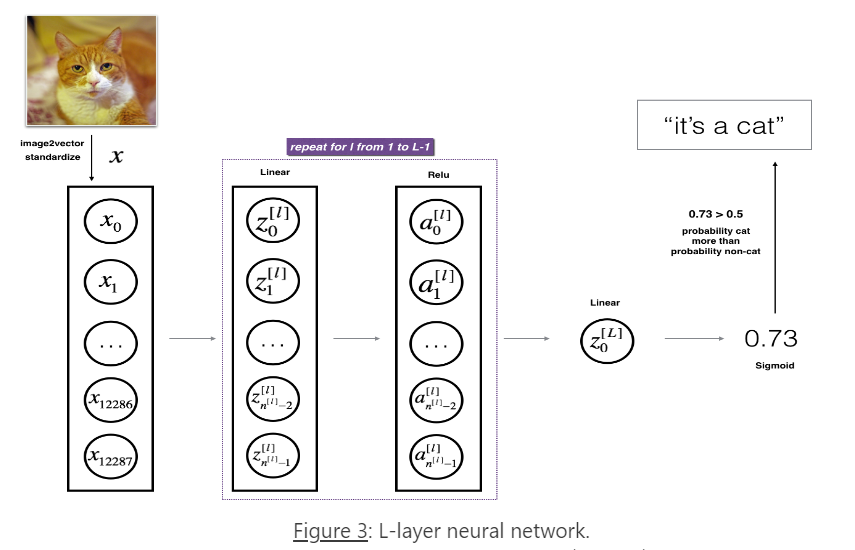
这个模型可以归纳为:
[LINEAR -> RELU]*(L-1) -> LINEAR -> SIGMOID
具体细节介绍:

4. Two-layer neural network实现
4.1定义基本功能
#初始化参数
def initialize_parameters(n_x,n_h,n_y):
np.random.seed(1)
W1 = np.random.randn(n_h,n_x)*0.01
b1 = np.zeros((n_h,1))
W2 = np.random.randn(n_y,n_h)*0.01
b2 = np.zeros((n_y,1))
#验证矩阵维度是否正确
assert((n_h, n_x) == W1.shape)
assert((n_h, 1) == b1.shape)
assert((n_y, n_h) == W2.shape)
assert((n_y, 1) == b2.shape)
#整合参数到parameters中输出
parameters = {
"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2
}
return parameters
#前向传播
def linear_activation_forward(A_prev, W, b, activation):
# 执行线性变换(矩阵乘法 + 偏置项)
if activation == "sigmoid":
# 计算 Z 和线性缓存
Z, linear_cache = linear_forward(A_prev, W, b)
# 应用 Sigmoid 激活函数并计算激活缓存
A, activation_cache = sigmoid(Z)
elif activation == "relu":
# 计算 Z 和线性缓存
Z, linear_cache = linear_forward(A_prev, W, b)
# 应用 ReLU 激活函数并计算激活缓存
A, activation_cache = relu(Z)
# 检查输出形状是否正确
assert(A.shape == (W.shape[0], A_prev.shape[1]))
# 将线性缓存和激活缓存组合在一起
cache = (linear_cache, activation_cache)
# 返回输出和缓存
return A, cache
#计算损失值
def compute_cost(AL,Y):
m = Y.shape[1]
cost = -(np.dot(np.log(AL), Y.T) + np.dot(np.log(1 - AL), (1 - Y).T)) / (1.0 * m)
cost = np.squeeze(cost)
assert(cost.shape==())
return cost
#反向传播
def linear_activation_backward(dA, cache, activation):
# 从缓存中获取线性缓存和激活缓存
linear_cache, activation_cache = cache
# 根据激活函数选择相应的反向传播函数
if activation == "relu":
# 计算ReLU激活函数的梯度
dZ = relu_backward(dA, activation_cache)
# 计算线性层的梯度
dA_prev, dW, db = linear_backward(dZ, linear_cache)
elif activation == "sigmoid":
# 计算Sigmoid激活函数的梯度
dZ = sigmoid_backward(dA, activation_cache)
# 计算线性层的梯度
dA_prev, dW, db = linear_backward(dZ, linear_cache)
# 返回各参数的梯度
return dA_prev, dW, db
#参数更新
def update_parameters(parameters, grads, learning_rate):
# 计算层数 L(不包括输入层)
L = len(parameters) // 2
# 遍历每一层
for i in range(1, L + 1):
# 更新权重矩阵 W
parameters["W" + str(i)] -= learning_rate * grads["dW" + str(i)]
# 更新偏置项 b
parameters["b" + str(i)] -= learning_rate * grads["db" + str(i)]
# 返回更新后的参数
return parameters
4.2定义模型参数
n_x = 12288 # num_px * num_px * 3
n_h = 7
n_y = 1
layers_dims = (n_x, n_h, n_y)
4.3Two-layer neural network定义
def two_layer_model(X,Y,layers_dims,learning_rate = 0.0075,num_iterations=3000,print_cost=False):
"""实现一个两层神经网络:LINEAR->RELU->LINEAR->SIGMOID.
参数:
X -- 输入数据,形状为 (n_x, 样本数量)
Y -- 真实标签向量(猫为 0,非猫为 1),形状为 (1, 样本数量)
layers_dims -- 层的维度 (n_x, n_h, n_y)
num_iterations -- 优化循环的迭代次数
learning_rate -- 梯度下降的 learning rate
print_cost -- 如果设为 True,将每 100 次迭代打印一次损失函数值
返回:
parameters -- 包含 W1, W2, b1, b2 的字典"""
np.random.seed(1)
grads = {}
costs = []
m = X.shape[1]
(n_x,n_h,n_y) = layers_dims
parameters = initialize_parameters(n_x,n_h,n_y)
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
for i in range(0,num_iterations):
#前向传播
A1,cache1 = linear_activation_forward(X,parameters["W1"],parameters["b1"],activation="relu")
A2,cache2 = linear_activation_forward(A1,parameters["W2"],parameters["b2"],activation="sigmoid")
#计算损失
cost = compute_cost(A2,Y)
#初始化反向传播
dA2 = - (np.divide(Y, A2) - np.divide(1 - Y, 1 - A2))
#反向传播:输入“dA2, cache2, cache1”,输出“dA1, dW2, db2; also dA0 (not used), dW1, db1”
dA1,dW2,db2 = linear_activation_backward(dA2,cache2,activation="sigmoid")
dA0,dW1,db1 = linear_activation_backward(dA1,cache1,activation="relu")
# 设置 grads['dWl'] 为 dW1, grads['db1'] 为 db1, grads['dW2'] 为 dW2, grads['db2'] 为 db2
grads['dW1'] = dW1
grads['db1'] = db1
grads['dW2'] = dW2
grads['db2'] = db2
#更新参数
parameters = update_parameters(parameters,grads,learning_rate)
#从新的参数中获取 W1, b1, W2, b2
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
#每训练100个样本输出一次损失值
if print_cost and i%100 == 0:
print("Cost after iteration {}: {}".format(i, np.squeeze(cost)))
if i % 100 == 0:
costs.append(cost)
if not(print_cost):
print("The final cost = %f" %(cost))
# 画出损失函数曲线
plt.plot(np.squeeze(costs))
plt.ylabel('cost')
plt.xlabel('iterations (per hundreds)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
return parameters
4.4运行该网络进行训练
parameters = two_layer_model(train_x, train_y, layers_dims = (n_x, n_h, n_y), num_iterations = 2500, print_cost=True)
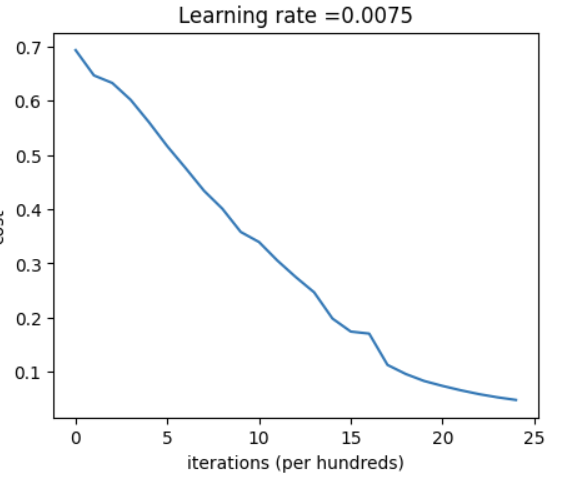
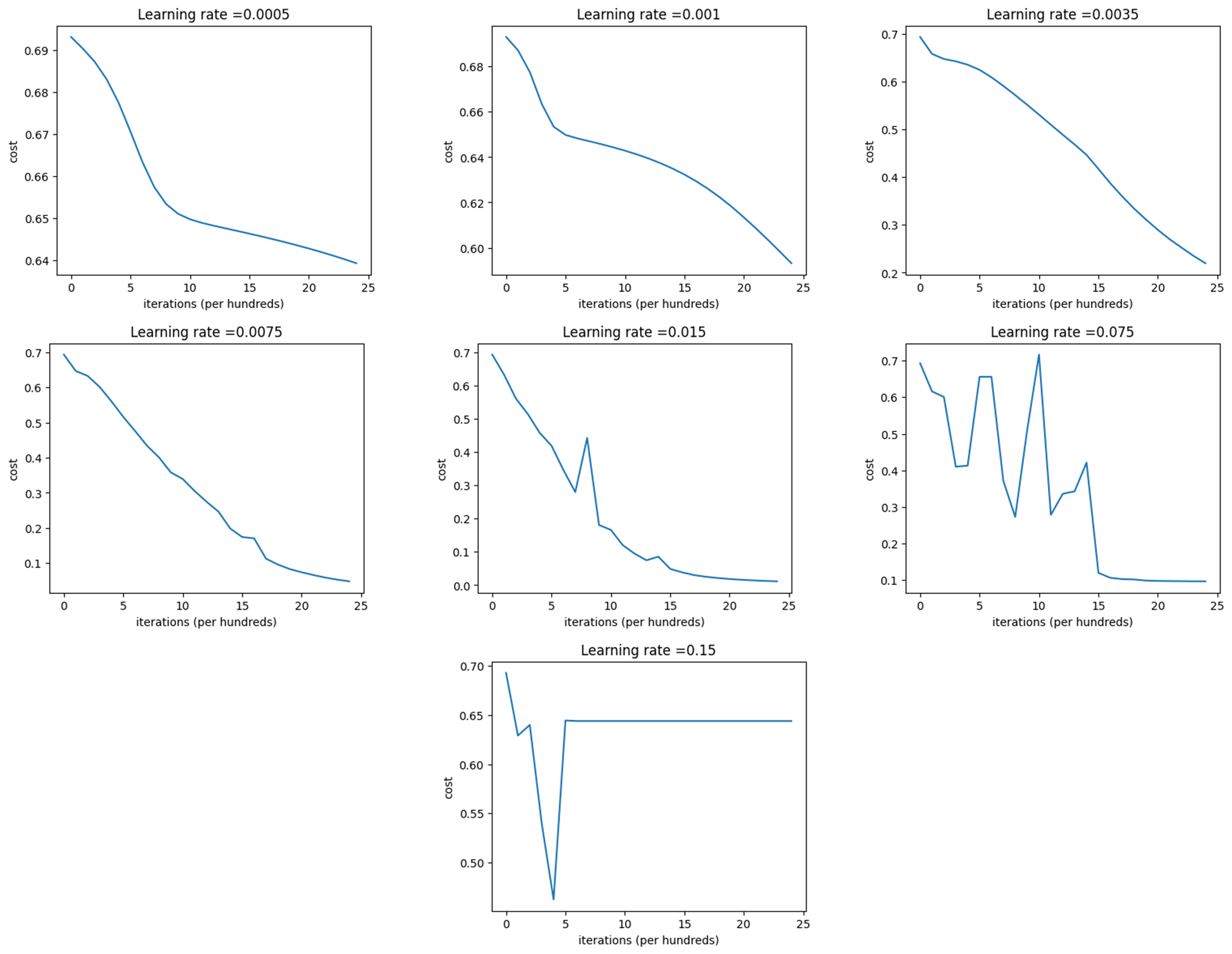
- 接着通过改变不同的学习率来寻找一个最合适的学习率来进行训练
print(datetime.datetime.now())
two_layer_model(train_x, train_y, layers_dims=(n_x, n_h, n_y), learning_rate=0.0005, num_iterations=2500, print_cost=False)
print(datetime.datetime.now())
two_layer_model(train_x, train_y, layers_dims=(n_x, n_h, n_y), learning_rate=0.0010, num_iterations=2500, print_cost=False)
print(datetime.datetime.now())
two_layer_model(train_x, train_y, layers_dims=(n_x, n_h, n_y), learning_rate=0.0035, num_iterations=2500, print_cost=False)
print(datetime.datetime.now())
two_layer_model(train_x, train_y, layers_dims=(n_x, n_h, n_y), learning_rate=0.0075, num_iterations=2500, print_cost=False)
print(datetime.datetime.now())
two_layer_model(train_x, train_y, layers_dims=(n_x, n_h, n_y), learning_rate=0.0150, num_iterations=2500, print_cost=False)
print(datetime.datetime.now())
two_layer_model(train_x, train_y, layers_dims=(n_x, n_h, n_y), learning_rate=0.0750, num_iterations=2500, print_cost=False)
print(datetime.datetime.now())
two_layer_model(train_x, train_y, layers_dims=(n_x, n_h, n_y), learning_rate=0.1500, num_iterations=2500, print_cost=False)
print(datetime.datetime.now())
4.5定义预测函数
def predict(X, y, parameters):
m = X.shape[1]
n = len(parameters) // 2
p = np.zeros((1, m))
probas, caches = L_model_forward(X, parameters)
for i in range(probas.shape[1]):
if probas[0,i] > 0.5:
p[0, i] = 1
else:
p[0, i] = 0
print("Accuracy: " + str(np.sum(p == y) / (1.0 * m)))
return p
4.6执行预测
predictions_train = predict(train_x, train_y, parameters)
predictions_test = predict(test_x, test_y, parameters)
结果:
1.0
0.72
我们可以注意到,在更少的迭代(比如1500次)上运行模型可以在测试集上获得更好的准确性。这被称为“提前停止”。提前停止是防止过拟合的一种方法。
该2层神经网络比逻辑回归实现(70%)有更好的性能(72%)。接着我们看看用$L$层模型是否可以做得更好。
5. L-layer Neural Network实现
5.1定义基本功能
def initialize_parameters_deep(layer_dims):
np.random.seed(1) # 设置随机种子,确保每次运行结果相同
parameters = {}
L = len(layer_dims) # 网络层数
for i in range(1, L):
# 注意,这里的标准差是 np.sqrt(layer_dims[i - 1]),而不是固定的0.01
parameters['W' + str(i)] = np.random.randn(layer_dims[i], layer_dims[i - 1]) / np.sqrt(layer_dims[i - 1])
parameters["b" + str(i)] = np.zeros((layer_dims[i], 1)) # 初始化偏置为0
# 确保权重和偏置的维度正确
assert((layer_dims[i], layer_dims[i - 1]) == parameters["W" + str(i)].shape)
assert((layer_dims[i], 1) == parameters["b" + str(i)].shape)
return parameters
def L_model_forward(X, parameters):
caches = []
A = X # 初始激活值设置为输入X
L = len(parameters) // 2 # 网络层数
for i in range(1, L):
A_prev = A # 上一层的激活值
# 前向传播,使用ReLU激活函数
A, cache = linear_activation_forward(A_prev, parameters["W" + str(i)], parameters["b" + str(i)], "relu")
caches.append(cache) # 保存缓存
# 最后一层使用sigmoid激活函数
AL, cache = linear_activation_forward(A, parameters["W" + str(L)], parameters["b" + str(L)], "sigmoid")
caches.append(cache)
# 确保输出AL的形状正确
assert(AL.shape == (1, X.shape[1]))
return AL, caches
def compute_cost(AL, Y):
m = Y.shape[1] # 样本数量
# 计算成本
cost = -(np.dot(np.log(AL), Y.T) + np.dot(np.log(1 - AL), (1 - Y).T)) / (m * 1.0)
cost = np.squeeze(cost) # 移除单维度条目
assert(cost.shape == ()) # 确保成本是标量
return cost
def L_model_backward(AL, Y, caches):
grads = {}
L = len(caches) # 网络层数
m = AL.shape[1] # 样本数量
Y = Y.reshape(AL.shape) # 调整Y的形状与AL相匹配
# 计算梯度
dAL = -(np.divide(Y, AL) - np.divide(1 - Y, 1 - AL))
# 反向传播的最后一层
current_cache = caches[L - 1]
grads["dA" + str(L)], grads["dW" + str(L)], grads["db" + str(L)] = linear_activation_backward(dAL, current_cache, activation="sigmoid")
# 反向传播的其他层
for i in reversed(range(L - 1)):
current_cache = caches[i]
dA_prev_temp, dW_temp, db_temp = linear_activation_backward(grads["dA" + str(i + 2)], current_cache, activation="relu")
grads["dA" + str(i + 1)] = dA_prev_temp
grads["dW" + str(i + 1)] = dW_temp
grads["db" + str(i + 1)] = db_temp
return grads
def update_parameters(parameters, grads, learning_rate):
L = len(parameters) // 2 # 网络层数
for i in range(1, L + 1):
# 使用梯度下降更新参数
parameters["W" + str(i)] -= learning_rate * grads["dW" + str(i)]
parameters["b" + str(i)] -= learning_rate * grads["db" + str(i)]
return parameters
5.2定义模型参数
layers_dims = [12288, 20, 7, 5, 1] # 5-layer model
5.3L_layer_model网络定义
def L_layer_model(X, Y, layers_dims, learning_rate = 0.0075, num_iterations = 3000, print_cost=False):
"""
实现一个L层神经网络: [LINEAR->RELU]*(L-1)->LINEAR->SIGMOID.
参数:
X -- 数据,形状为 (样本数, num_px * num_px * 3) 的numpy数组
Y -- 真实的“标签”向量(如果是猫则为0,不是猫则为1),形状为 (1, 样本数)
layers_dims -- 包含输入大小和每层大小的列表,长度为 (层数 + 1)
learning_rate -- 梯度下降更新规则的学习率
num_iterations -- 优化循环的迭代次数
print_cost -- 如果为True,则每100步打印一次成本
返回:
parameters -- 模型学习到的参数。它们可以用于预测。
"""
np.random.seed(1) # 设置随机种子以保持结果的一致性
costs = [] # 记录成本
# 参数初始化
parameters = initialize_parameters_deep(layers_dims)
# 梯度下降循环
for i in range(0, num_iterations):
# 前向传播: [LINEAR -> RELU]*(L-1) -> LINEAR -> SIGMOID
AL, caches = L_model_forward(X, parameters)
# 计算成本
cost = compute_cost(AL, Y)
# 反向传播
grads = L_model_backward(AL, Y, caches)
# 更新参数
parameters = update_parameters(parameters, grads, learning_rate)
# 每100个训练样本打印成本
if print_cost and i % 100 == 0:
print ("迭代次数 %i 后的成本: %f" %(i, cost))
if print_cost and i % 100 == 0:
costs.append(cost)
# 绘制成本曲线
plt.plot(np.squeeze(costs))
plt.ylabel('成本')
plt.xlabel('迭代次数(每十个)')
plt.title("学习率 = " + str(learning_rate))
plt.show()
return parameters
5.4运行该网络进行训练
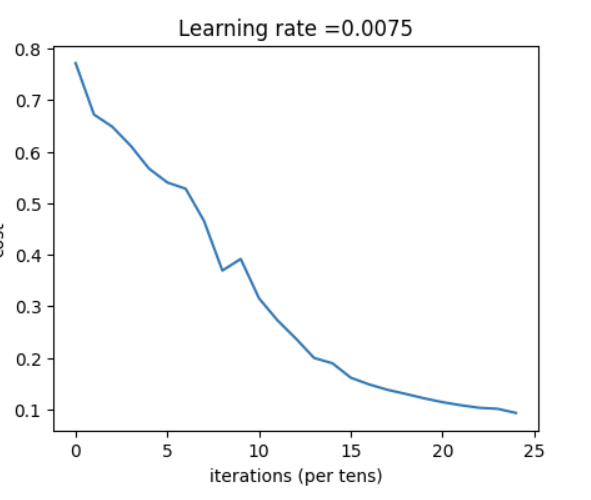
parameters = L_layer_model(train_x,train_y,layers_dims,num_iterations=2500,print_cost=True)
5.5执行预测
pred_train = predict(train_x, train_y, parameters)
pred_test = predict(test_x, test_y, parameters)
结果:
Accuracy: 0.9856459330143539
Accuracy: 0.8
该网络比4.3提到的网络测试集准确率提高了8%的准确率。
我们也可以利用print_mislabeled_images函数来看被L_layer网络错误分类的图片。
print_mislabeled_images(classes, test_x, test_y, pred_test)
