1.任务
分步构建卷积神经网络并进行部署应用。
2.Convolutional Neural Networks: Step by Step
符号说明:
- 上标 $[l]$ 表示第 $l^{th}$ 层的对象。
- 示例:$a^{[4]}$ 是第 $4^{th}$ 层的激活。$W^{[5]}$ 和 $b^{[5]}$ 是第 $5^{th}$ 层的参数。
- 上标 $(i)$ 表示来自第 $i^{th}$ 个示例的对象。
- 示例:$x^{(i)}$ 是第 $i^{th}$ 个训练示例输入。
- 下标 $i$ 表示向量的第 $i^{th}$ 个条目。
- 示例:$a^{[l]}_i$ 表示第 $l$ 层激活中的第 $i^{th}$ 个条目,假设这是一个全连接(FC)层。
- $n_H$、$n_W$ 和 $n_C$ 分别表示给定层的高度、宽度和通道数。如果你想引用特定的层 $l$,你也可以写成 $n_H^{[l]}$、$n_W^{[l]}$、$n_C^{[l]}$。
- $n_{H_{prev}}$、$n_{W_{prev}}$ 和 $n_{C_{prev}}$ 分别表示前一层的高度、宽度和通道数。如果引用特定层 $l$,这也可以表示为 $n_H^{[l-1]}$、$n_W^{[l-1]}$、$n_C^{[l-1]}$。
卷积神经网络的构建块要实现的每个函数的说明步骤:
- 卷积函数,包括:
- 零填充
- 卷积窗口
- 卷积前向传播
- 卷积反向传播(可选)
- 池化函数,包括:
- 池化前向传播
- 创建掩码
- 分配值
- 池化反向传播(可选)
2.1导入库
import numpy as np
import h5py
import matplotlib.pyplot as plt
np.random.seed(1)
2.2构建网络块
2.2.1Zero-Padding(零填充)
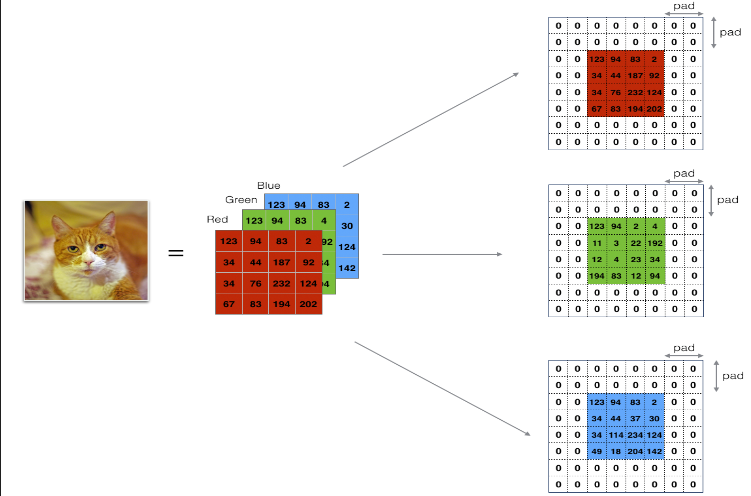
主要好处如下:
-
它允许你使用卷积层而不必缩小体积的高度和宽度。这对于构建更深的网络非常重要,因为否则在进入更深层次时,高度/宽度会缩小。一个重要的特例是“相同”卷积,在这种卷积中,经过一层处理后,高度/宽度被完全保留。
-
它帮助我们保留了图像边缘处更多的信息。如果没有填充,图像边缘的像素会对下一层的很少数值产生影响。
代码:
# 评分函数:zero_pad
def zero_pad(X, pad):
"""
在数据集 X 的所有图像上用零进行填充。填充应用于图像的高度和宽度,
如图 1 所示。
参数:
X -- 代表 m 张图像的一批的 python numpy 数组,形状为 (m, n_H, n_W, n_C)
pad -- 整数,每个图像在垂直和水平维度上的填充量
返回:
X_pad -- 填充后的图像,形状为 (m, n_H + 2*pad, n_W + 2*pad, n_C)
"""
### 开始编写代码 ### (≈ 1 行)
X_pad = np.pad(X, ((0,0), (pad,pad), (pad,pad), (0,0)), "constant")
### 结束编写代码 ###
return X_pad
部署:
np.random.seed(1)
x = np.random.randn(4, 3, 3, 2)
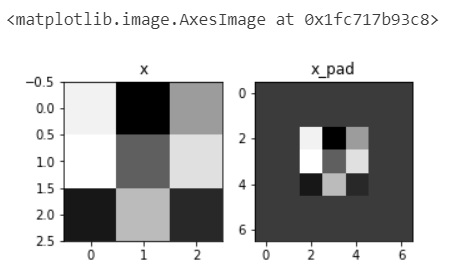
x_pad = zero_pad(x, 2)
print ("x.shape =", x.shape)
print ("x_pad.shape =", x_pad.shape)
print ("x[1,1] =", x[1,1])
print ("x_pad[1,1] =", x_pad[1,1])
fig, axarr = plt.subplots(1, 2)
axarr[0].set_title('x')
axarr[0].imshow(x[0,:,:,0])
axarr[1].set_title('x_pad')
axarr[1].imshow(x_pad[0,:,:,0])
输出:
x.shape = (4, 3, 3, 2)
x_pad.shape = (4, 7, 7, 2)
x[1,1] = [[ 0.90085595 -0.68372786]
[-0.12289023 -0.93576943]
[-0.26788808 0.53035547]]
x_pad[1,1] = [[0. 0.]
[0. 0.]
[0. 0.]
[0. 0.]
[0. 0.]
[0. 0.]
[0. 0.]]
2.2.2Convolve window(卷积窗口)
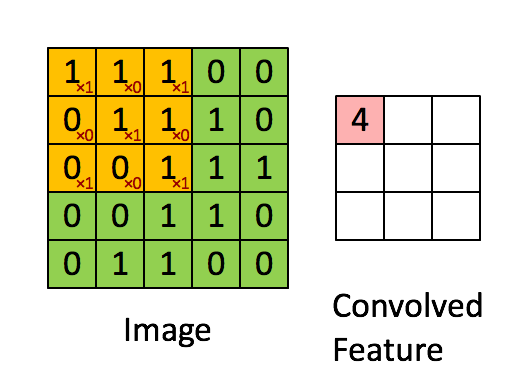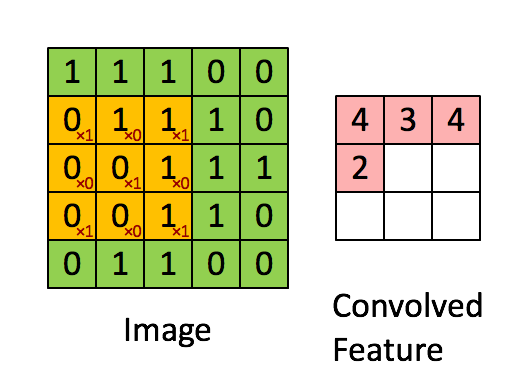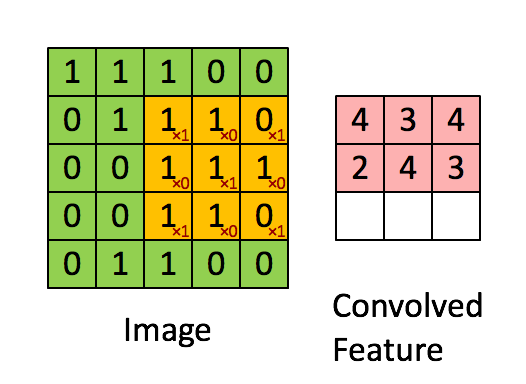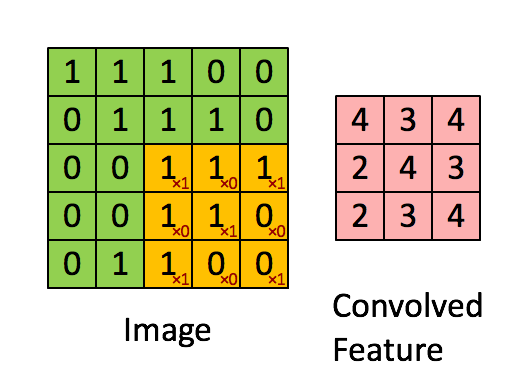
代码:
# 评分函数:conv_single_step
def conv_single_step(a_slice_prev, W, b):
"""
在前一层的输出激活的一个切片 (a_slice_prev) 上应用由参数 W 定义的一个过滤器。
参数:
a_slice_prev -- 输入数据的切片,形状为 (f, f, n_C_prev)
W -- 窗口中包含的权重参数 - 形状为 (f, f, n_C_prev) 的矩阵
b -- 窗口中包含的偏置参数 - 形状为 (1, 1, 1) 的矩阵
返回:
Z -- 一个标量值,输入数据的一个切片 x 上卷积滑动窗口 (W, b) 的结果
"""
### 开始编写代码 ### (≈ 2 行代码)
# a_slice 和 W 之间的元素级别乘积。暂时不要添加偏置。
s = np.multiply(a_slice_prev, W)
# 对体积 s 的所有条目求和。
Z = np.sum(s)
# 将偏置 b 添加到 Z 上。将 b 转换为 float(),使 Z 结果为一个标量值。
Z = Z + float(b)
### 结束编写代码 ###
return Z
部署:
np.random.seed(1)
a_slice_prev = np.random.randn(4, 4, 3)
W = np.random.randn(4, 4, 3)
b = np.random.randn(1, 1, 1)
Z = conv_single_step(a_slice_prev, W, b)
print("Z =", Z)
输出:
Z = -6.999089450680221
2.2.3Convolution forward(卷积前向传播)
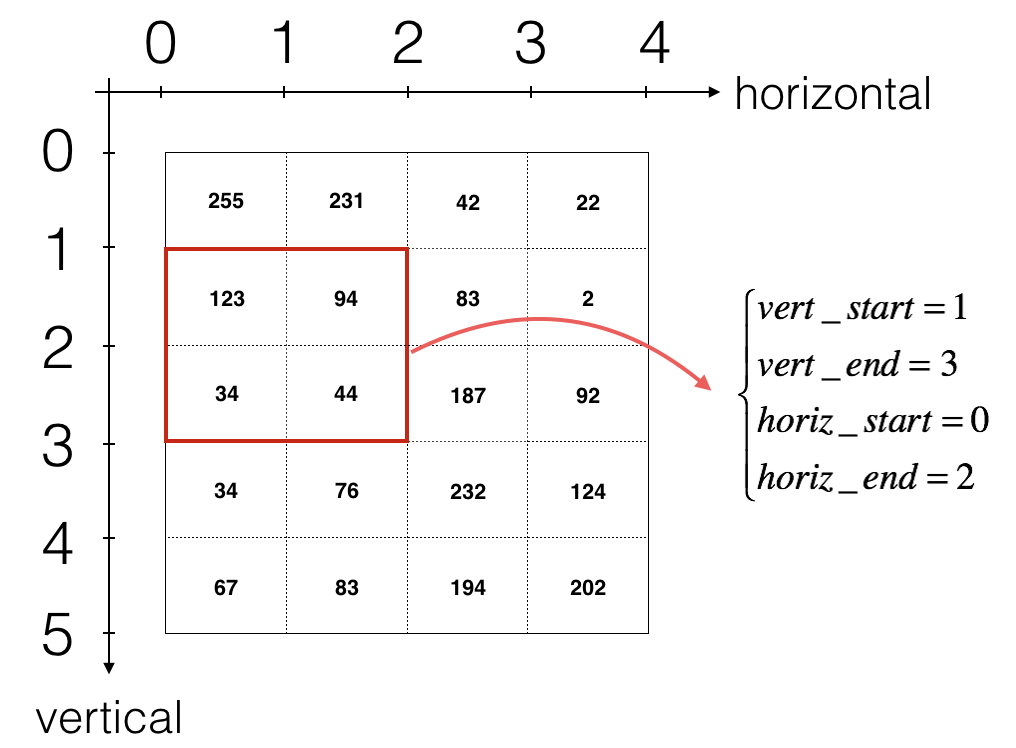
上图只显示单个通道,使用垂直和水平起止(使用 2x2 滤波器)定义切片
卷积的输出形状与输入形状相关的公式是: \(\left\{ \begin{aligned}n_H = \lfloor \frac{n_{H_{prev}} - f + 2 \times pad}{stride} \rfloor +1 \\ n_W = \lfloor \frac{n_{W_{prev}} - f + 2 \times pad}{stride} \rfloor +1 \\ n_C = \text{卷积中使用的滤波器数量}\end{aligned} \right.\)
# 评分函数:conv_forward
def conv_forward(A_prev, W, b, hparameters):
"""
实现卷积函数的前向传播
参数:
A_prev -- 前一层的输出激活,形状为 (m, n_H_prev, n_W_prev, n_C_prev) 的 numpy 数组
W -- 权重,形状为 (f, f, n_C_prev, n_C) 的 numpy 数组
b -- 偏置,形状为 (1, 1, 1, n_C) 的 numpy 数组
hparameters -- 包含 "stride" 和 "pad" 的 python 字典
返回:
Z -- 卷积输出,形状为 (m, n_H, n_W, n_C) 的 numpy 数组
cache -- conv_backward() 函数所需的值的缓存
"""
### 开始编写代码 ###
# 从 A_prev 的形状中检索维度 (≈1 行)
(m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape
# 从 W 的形状中检索维度 (≈1 行)
(f, f, n_C_prev, n_C) = W.shape
# 从 "hparameters" 中检索信息 (≈2 行)
stride = hparameters["stride"]
pad = hparameters["pad"]
# 使用上面给出的公式计算 CONV 输出体积的维度。提示:使用 int() 进行向下取整。 (≈2 行)
n_H = (n_H_prev - f + 2 * pad) // stride + 1
n_W = (n_W_prev - f + 2 * pad) // stride + 1
# 使用零初始化输出体积 Z。 (≈1 行)
Z = np.zeros((m, n_H, n_W, n_C))
# 通过填充 A_prev 来创建 A_prev_pad
A_prev_pad = zero_pad(A_prev, pad)
for i in range(m): # 遍历训练样本批次
a_prev_pad = A_prev_pad[i, :, :, :] # 选择第 i 个训练样本的填充激活
for h in range(n_H): # 遍历输出体积的垂直轴
for w in range(n_W): # 遍历输出体积的水平轴
for c in range(n_C): # 遍历输出体积的通道(= #过滤器)
# 找到当前“切片”的四个角 (≈4 行)
vert_start = h * stride
vert_end = vert_start + stride
horiz_start = w * stride
horiz_end = horiz_start + stride
# 使用角落来定义 a_prev_pad 的(3D)切片 (参见单元格上方的提示)。 (≈1 行)
a_slice_prev = a_prev_pad[vert_start : vert_end, horiz_start : horiz_end, : ]
# 用正确的过滤器 W 和偏置 b 对(3D)切片进行卷积,以得到一个输出神经元。 (≈1 行)
Z[i, h, w, c] = conv_single_step(a_slice_prev, W[:, :, :, c], b[:, :, :, c])
### 结束编写代码 ###
# 确保输出形状是正确的
assert(Z.shape == (m, n_H, n_W, n_C))
# 在 "cache" 中保存反向传播所需的信息
cache = (A_prev, W, b, hparameters)
return Z, cache
部署:
#生成样例数据
np.random.seed(1)
A_prev = np.random.randn(10,4,4,3)
W = np.random.randn(2,2,3,8)
b = np.random.randn(1,1,1,8)
hparameters = {"pad" : 2,
"stride": 2}
#部署
Z, cache_conv = conv_forward(A_prev, W, b, hparameters)
print("Z's mean =", np.mean(Z))
print("Z[3,2,1] =", Z[3,2,1])
print("cache_conv[0][1][2][3] =", cache_conv[0][1][2][3])
输出:
Z's mean = 0.048995203528855794
Z[3,2,1] = [-0.61490741 -6.7439236 -2.55153897 1.75698377 3.56208902 0.53036437
5.18531798 8.75898442]
cache_conv[0][1][2][3] = [-0.20075807 0.18656139 0.41005165]
2.2.4Convolution backward(卷积反向传播)
- 计算dA
这是计算相对于某一特定滤波器 $W_c$ 和一个给定训练样本的成本的 $dA$ 的公式:
\[dA += \sum _{h=0} ^{n_H} \sum_{w=0} ^{n_W} W_c \times dZ_{hw} \tag{1}\] 其中 $W_c$ 是一个滤波器,$dZ_{hw}$ 是一个标量,对应于卷积层 Z 的输出在第 h 行和第 w 列的成本梯度(对应于在第 i 个步长向左和第 j 个步长向下时取的点积)。注意,每次我们都用相同的滤波器 $W_c$ 乘以不同的 dZ 来更新 dA。这主要是因为在计算前向传播时,每个滤波器都由不同的 a_slice 点乘并求和。因此,在计算 dA 的反向传播时,我们只是添加所有 a_slices 的梯度。
在代码中,放在适当的 for 循环内,这个公式转化为:
da_prev_pad[vert_start:vert_end, horiz_start:horiz_end, :] += W[:,:,:,c] * dZ[i, h, w, c]
- 计算dW
这是计算相对于损失的 $dW_c$($dW_c$ 是一个滤波器的导数)的公式:
\(dW_c += \sum _{h=0} ^{n_H} \sum_{w=0} ^ {n_W} a_{slice} \times dZ_{hw} \tag{2}\) 其中 $a_{slice}$ 对应于用于生成激活 $Z_{ij}$ 的切片。因此,这最终给我们提供了关于该切片的 $W$ 的梯度。由于是相同的 $W$,我们将简单地将所有这些梯度相加,以获得 $dW$。
在代码中,放在适当的 for 循环内,这个公式转化为:
dW[:,:,:,c] += a_slice * dZ[i, h, w, c]
- 计算db
这是计算相对于某一特定滤波器 $W_c$ 的成本的 $db$ 的公式:
\(db = \sum_h \sum_w dZ_{hw} \tag{3}\) 正如你在基础神经网络中之前所见,$db$ 是通过求和 $dZ$ 来计算的。在这种情况下,你只是对卷积输出 (Z) 相对于成本的所有梯度求和。
在代码中,放在适当的 for 循环内,这个公式转化为:
db[:,:,:,c] += dZ[i, h, w, c]
代码:
def conv_backward(dZ, cache):
"""
实现卷积函数的反向传播
参数:
dZ -- 相对于卷积层输出 (Z) 的成本梯度,形状为 (m, n_H, n_W, n_C) 的 numpy 数组
cache -- conv_backward() 所需的值的缓存,conv_forward() 的输出
返回:
dA_prev -- 相对于卷积层输入 (A_prev) 的成本梯度,
形状为 (m, n_H_prev, n_W_prev, n_C_prev) 的 numpy 数组
dW -- 相对于卷积层权重 (W) 的成本梯度,
形状为 (f, f, n_C_prev, n_C) 的 numpy 数组
db -- 相对于卷积层偏置 (b) 的成本梯度,
形状为 (1, 1, 1, n_C) 的 numpy 数组
"""
### 开始编写代码 ###
# 从 "cache" 中检索信息
(A_prev, W, b, hparameters) = cache
# 从 A_prev 的形状中检索维度
(m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape
# 从 W 的形状中检索维度
(f, f, n_C_prev, n_C) = W.shape
# 从 "hparameters" 中检索信息
stride = hparameters["stride"]
pad = hparameters["pad"]
# 从 dZ 的形状中检索维度
(m, n_H, n_W, n_C) = dZ.shape
# 使用正确的形状初始化 dA_prev, dW, db
dA_prev = np.zeros((m, n_H_prev, n_W_prev, n_C_prev))
dW = np.zeros((f, f, n_C_prev, n_C))
db = np.zeros((1, 1, 1, n_C))
# 对 A_prev 和 dA_prev 进行填充
A_prev_pad = zero_pad(A_prev, pad)
dA_prev_pad = zero_pad(dA_prev, pad)
for i in range(m): # 遍历训练样本
# 从 A_prev_pad 和 dA_prev_pad 中选择第 i 个训练样本
a_prev_pad = A_prev_pad[i, :, :, :]
da_prev_pad = dA_prev_pad[i, :, :, :]
for h in range(n_H): # 在输出体积的垂直轴上遍历
for w in range(n_W): # 在输出体积的水平轴上遍历
for c in range(n_C): # 遍历输出体积的通道
# 找到当前“切片”的角落
vert_start = h * stride
vert_end = vert_start + f
horiz_start = w * stride
horiz_end = horiz_start + f
# 使用角落来定义 a_prev_pad 的切片
a_slice = a_prev_pad[vert_start : vert_end, horiz_start : horiz_end, :]
# 使用上面给出的公式更新窗口和过滤器参数的梯度
da_prev_pad[vert_start:vert_end, horiz_start:horiz_end, :] += W[:, :, :, c] * dZ[i, h, w, c]
dW[:,:,:,c] += a_slice * dZ[i, h, w, c]
db[:,:,:,c] += dZ[i, h, w, c]
# 将第 i 个训练样本的 dA_prev 设置为未填充的 da_prev_pad(提示:使用 X[pad:-pad, pad:-pad, :])
dA_prev[i, :, :, :] = da_prev_pad[pad : -pad, pad : -pad, :]
### 结束编写代码 ###
# 确保输出形状是正确的
assert(dA_prev.shape == (m, n_H_prev, n_W_prev, n_C_prev))
return dA_prev, dW, db
部署:
np.random.seed(1)
dA, dW, db = conv_backward(Z, cache_conv)
print("dA_mean =", np.mean(dA))
print("dW_mean =", np.mean(dW))
print("db_mean =", np.mean(db))
输出:
dA_mean = 1.4524377775388075
dW_mean = 1.7269914583139097
db_mean = 7.839232564616838
2.2.5Pooling forward(池化前向传播)
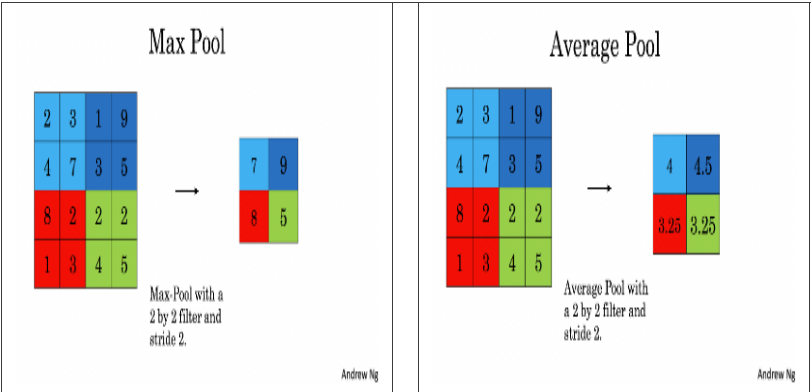
由于没有填充,将池化的输出形状与输入形状绑定的公式是:
$$ \left{ \begin{aligned} n_H = \lfloor \frac{n_{H_{prev}} - f}{stride} \rfloor +1\
n_W = \lfloor \frac{n_{W_{prev}} - f}{stride} \rfloor +1
n_C = n_{C_{prev}}
\end{aligned}
\right.
$$
代码:
# 评分函数:pool_forward
def pool_forward(A_prev, hparameters, mode = "max"):
"""
实现池化层的前向传播
参数:
A_prev -- 输入数据,形状为 (m, n_H_prev, n_W_prev, n_C_prev) 的 numpy 数组
hparameters -- 包含 "f" 和 "stride" 的 python 字典
mode -- 您想要使用的池化模式,定义为一个字符串("max" 或 "average")
返回:
A -- 池化层的输出,形状为 (m, n_H, n_W, n_C) 的 numpy 数组
cache -- 在池化层的反向传播中使用的缓存,包含输入和 hparameters
"""
# 从输入形状中检索维度
(m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape
# 从 "hparameters" 中检索超参数
f = hparameters["f"]
stride = hparameters["stride"]
# 定义输出的维度
n_H = int(1 + (n_H_prev - f) / stride)
n_W = int(1 + (n_W_prev - f) / stride)
n_C = n_C_prev
# 初始化输出矩阵 A
A = np.zeros((m, n_H, n_W, n_C))
### 开始编写代码 ###
for i in range(m): # 遍历训练样本
for h in range(n_H): # 在输出体积的垂直轴上遍历
for w in range(n_W): # 在输出体积的水平轴上遍历
for c in range (n_C): # 遍历输出体积的通道
# 找到当前“切片”的角落 (≈4 行)
vert_start = h * stride
vert_end = vert_start + f
horiz_start = w * stride
horiz_end = horiz_start + f
# 使用角落来定义 A_prev 的第 i 个训练样本上的当前切片,通道 c。 (≈1 行)
a_prev_slice = A_prev[i, vert_start : vert_end, horiz_start : horiz_end, c]
# 在切片上计算池化操作。使用 if 语句区分模式。使用 np.max/np.mean。
if mode == "max":
A[i, h, w, c] = np.max(a_prev_slice)
elif mode == "average":
A[i, h, w, c] = np.mean(a_prev_slice)
### 结束编写代码 ###
# 为 pool_backward() 存储输入和 hparameters 在 "cache" 中
cache = (A_prev, hparameters)
# 确保输出形状是正确的
assert(A.shape == (m, n_H, n_W, n_C))
return A, cache
部署:
np.random.seed(1)
A_prev = np.random.randn(2, 4, 4, 3)
hparameters = {"stride" : 2, "f": 3}
A, cache = pool_forward(A_prev, hparameters)
print("mode = max")
print("A =", A)
print()
A, cache = pool_forward(A_prev, hparameters, mode = "average")
print("mode = average")
print("A =", A)
输出:
mode = max
A = [[[[1.74481176 0.86540763 1.13376944]]]
[[[1.13162939 1.51981682 2.18557541]]]]
mode = average
A = [[[[ 0.02105773 -0.20328806 -0.40389855]]]
[[[-0.22154621 0.51716526 0.48155844]]]]
2.2.6Pooling backward(池化反向传播)
在跳入池化层的反向传播之前,你将构建一个名为 create_mask_from_window() 的辅助函数,它执行以下操作:
如你所见,这个函数创建了一个“掩码”矩阵,用来追踪矩阵中的最大值位置。真(1)表示 X 中最大值的位置,其它条目为假(0)。你稍后会看到,平均池化的反向传播过程与此类似,但使用的掩码不同。
1.辅助函数代码:
def create_mask_from_window(x):
"""
从输入矩阵 x 创建一个掩码,用于标识 x 的最大条目。
参数:
x -- 形状为 (f, f) 的数组
返回:
mask -- 与窗口形状相同的数组,在与 x 的最大条目相对应的位置包含一个 True。
"""
### 开始编写代码 ### (≈1 行)
mask = (x >= np.max(x))
### 结束编写代码 ###
return mask
部署:
np.random.seed(1)
x = np.random.randn(2,3)
mask = create_mask_from_window(x)
print('x = ', x)
print("mask = ", mask)
输出:
x = [[ 1.62434536 -0.61175641 -0.52817175]
[-1.07296862 0.86540763 -2.3015387 ]]
mask = [[ True False False]
[False False False]]
2.反向传播 backward pass 算法代码:
在最大池化中,对于每个输入窗口,所有对输出的“影响”都来自单个输入值——最大值。在平均池化中,输入窗口的每个元素对输出都有相同的影响。因此,为了实现反向传播,你现在将实现一个反映这一点的辅助函数。
例如,如果我们在前向传播中使用 2x2 滤波器进行平均池化,那么你在反向传播中使用的掩码将看起来像: \(dZ = 1 \quad \rightarrow \quad dZ =\begin{bmatrix} 1/4 && 1/4 \\ 1/4 && 1/4 \end{bmatrix}\tag{5}\)
这意味着 $dZ$ 矩阵中的每个位置都平等地贡献于输出,因为在前向传播中,我们取了平均值。
def distribute_value(dz, shape):
"""
在维度为 shape 的矩阵中分布输入值
参数:
dz -- 输入标量
shape -- 我们想要分布 dz 值的输出矩阵的形状 (n_H, n_W)
返回:
a -- 大小为 (n_H, n_W) 的数组,我们在其中分布了 dz 的值
"""
### 开始编写代码 ###
# 从 shape 中检索维度 (≈1 行)
(n_H, n_W) = shape
# 计算在矩阵上分布的值 (≈1 行)
average = dz / (n_H * n_W)
# 创建一个每个条目都是 "average" 值的矩阵 (≈1 行)
a = average * np.ones((n_H, n_W))
### 结束编写代码 ###
return a
部署:
a = distribute_value(2, (2,2))
print('distributed value =', a)
输出:
distributed value = [[0.5 0.5]
[0.5 0.5]]
- 3.反向传播 Pooling backward 算法代码:
def pool_backward(dA, cache, mode = "max"):
"""
实现池化层的反向传播
参数:
dA -- 相对于池化层输出的成本梯度,与 A 的形状相同
cache -- 来自池化层前向传播的缓存输出,包含层的输入和 hparameters
mode -- 您想要使用的池化模式,定义为字符串("max" 或 "average")
返回:
dA_prev -- 相对于池化层输入的成本梯度,与 A_prev 的形状相同
"""
### 开始编写代码 ###
# 从缓存中检索信息 (≈1 行)
(A_prev, hparameters) = cache
# 从 "hparameters" 中检索超参数 (≈2 行)
stride = hparameters["stride"]
f = hparameters["f"]
# 从 A_prev 的形状和 dA 的形状中检索维度 (≈2 行)
m, n_H_prev, n_W_prev, n_C_prev = A_prev.shape
m, n_H, n_W, n_C = dA.shape
# 使用零初始化 dA_prev (≈1 行)
dA_prev = np.zeros((A_prev.shape))
for i in range(m): # 遍历训练样本
# 从 A_prev 中选择训练样本 (≈1 行)
a_prev = A_prev[i, :, :, :]
for h in range(n_H): # 在垂直轴上遍历
for w in range(n_W): # 在水平轴上遍历
for c in range(n_C): # 遍历通道(深度)
# 找到当前“切片”的角落 (≈4 行)
vert_start = h * stride
vert_end = vert_start + f
horiz_start = w * stride
horiz_end = horiz_start + f
# 在两种模式下计算反向传播。
if mode == "max":
# 使用角落和 "c" 来定义来自 a_prev 的当前切片 (≈1 行)
a_prev_slice = a_prev[vert_start : vert_end, horiz_start : horiz_end, c]
# 从 a_prev_slice 创建掩码 (≈1 行)
mask = create_mask_from_window(a_prev_slice)
# 将 dA_prev 设置为 dA_prev + (掩码乘以 dA 的正确条目) (≈1 行)
dA_prev[i, vert_start: vert_end, horiz_start: horiz_end, c] += dA[i, h, w, c] * mask
elif mode == "average":
# 从 dA 获取值 da (≈1 行)
da = dA[i, h, w, c]
# 定义过滤器的形状为 fxf (≈1 行)
shape = (f, f)
# 分布它以获得 dA_prev 的正确切片。即添加 da 的分布值。 (≈1 行)
dA_prev[i, vert_start: vert_end, horiz_start: horiz_end, c] += distribute_value(da, shape)
### 结束编写代码 ###
# 确保输出形状是正确的
assert(dA_prev.shape == A_prev.shape)
return dA_prev
部署:
np.random.seed(1)
A_prev = np.random.randn(5, 5, 3, 2)
hparameters = {"stride" : 1, "f": 2}
A, cache = pool_forward(A_prev, hparameters)
dA = np.random.randn(5, 4, 2, 2)
dA_prev = pool_backward(dA, cache, mode = "max")
print("mode = max")
print('mean of dA = ', np.mean(dA))
print('dA_prev[1,1] = ', dA_prev[1,1])
print()
dA_prev = pool_backward(dA, cache, mode = "average")
print("mode = average")
print('mean of dA = ', np.mean(dA))
print('dA_prev[1,1] = ', dA_prev[1,1])
输出:
mode = max
mean of dA = 0.14571390272918056
dA_prev[1,1] = [[ 0. 0. ]
[ 5.05844394 -1.68282702]
[ 0. 0. ]]
mode = average
mean of dA = 0.14571390272918056
dA_prev[1,1] = [[ 0.08485462 0.2787552 ]
[ 1.26461098 -0.25749373]
[ 1.17975636 -0.53624893]]
3.Convolutional Neural Networks: Application
https://github.com/dennybritz/cnn-text-classification-tf