1.目标
学习RNN的基本结构,并以此延伸出来的现代循环神经网络:GRU、LSTM、深度循环神经网络、双向循环神经网络、编码器-解码器结构、序列到序列学习(seq2seq)、束搜索。
通过自己大致复现一遍经典循环神经网络结构,熟悉代码的架构和模板。这里基础知识尽可能精简,多写一些模型和不同方法适用的场景。
2.Basic RNN Structure
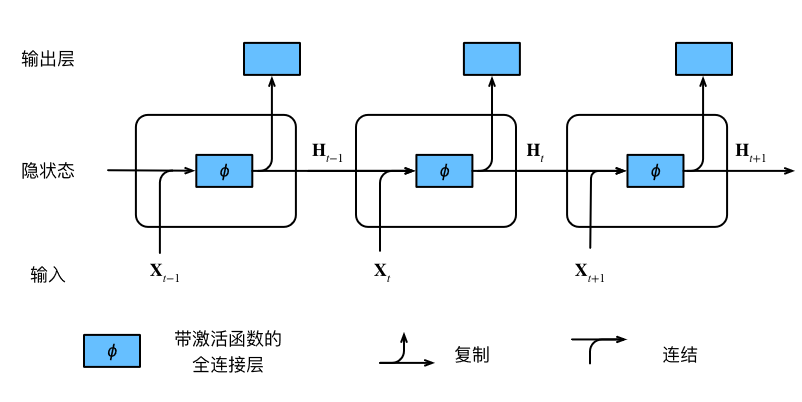
利用Pytorch框架的高级API简洁实现RNN网络,最后利用困惑度指标来进行评价模型的训练情况。
- 导入库并下载数据集:
1 | import torch |
- 定义模型及其参数:
1 | #构造一个256个隐藏单元的单隐藏层的RNN |
- 训练及预测:
1 | #训练和预测 |
- 输出:
1 | perplexity 1.0, 503854.1 tokens/sec on cuda:0 |
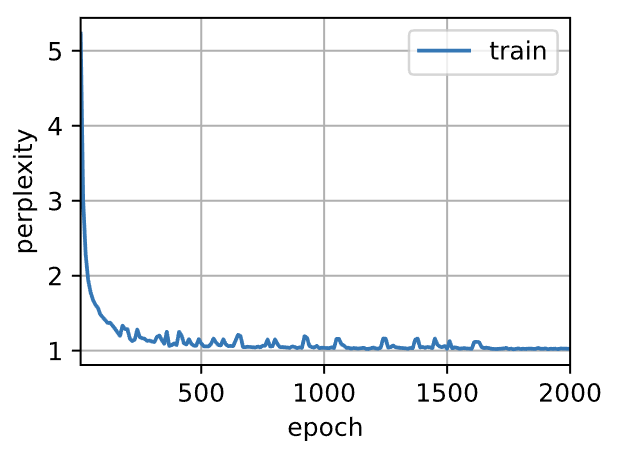
注意:高级API的循环神经网络返回一个输出和一个更新后的隐状态,我们还要计算整个模型的输出层。
3.Modern RNN Structure
3.1GRU
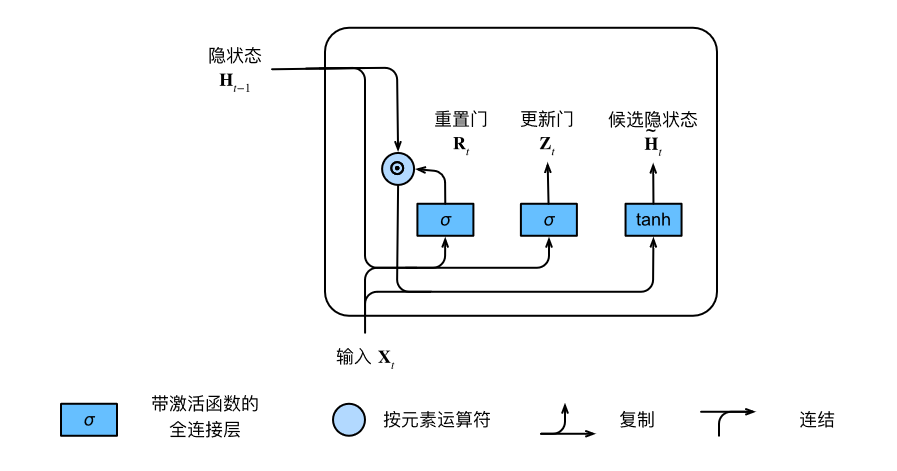
- 重置门、更新门、候选隐状态、隐状态
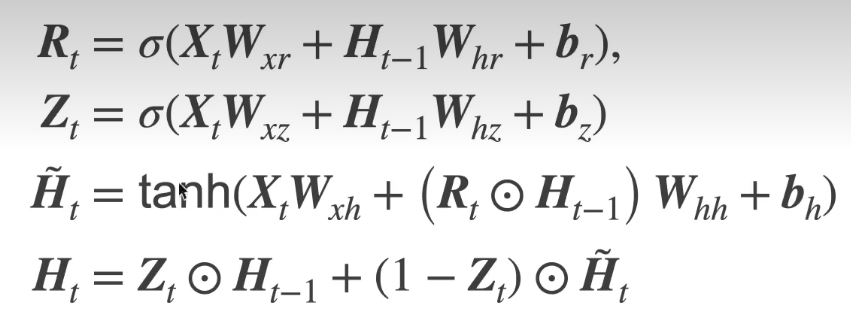
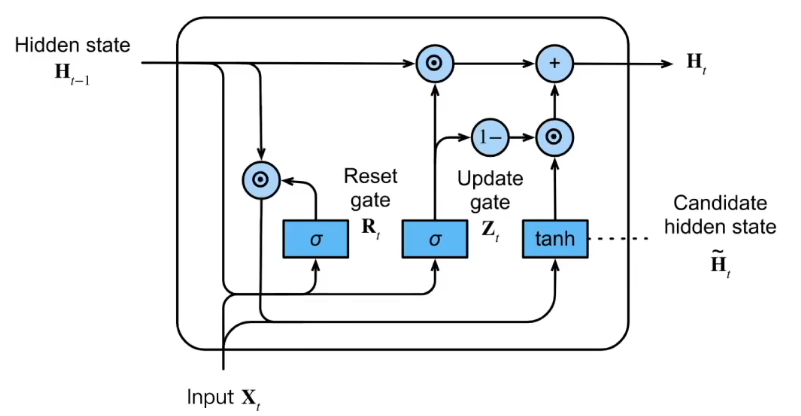
代码实现:
- 导入依赖库:
1 | import torch |
- 初始化模型参数并定义模型:
1 | #初始化模型参数 |
- 训练预测:
1 | #训练和预测 |
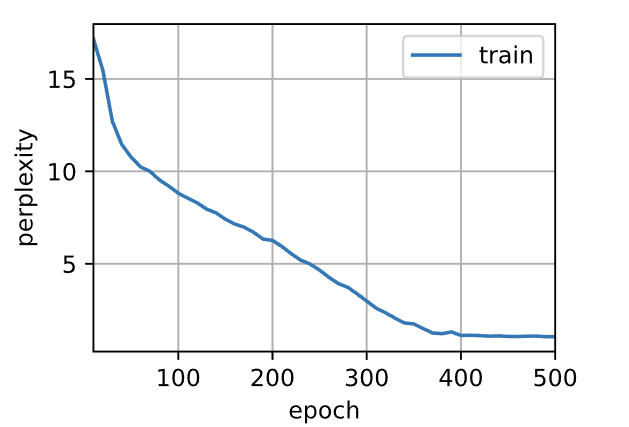
- 输出:
1 | perplexity 1.1, 27726.3 tokens/sec on cuda:0 |
3.2LSTM
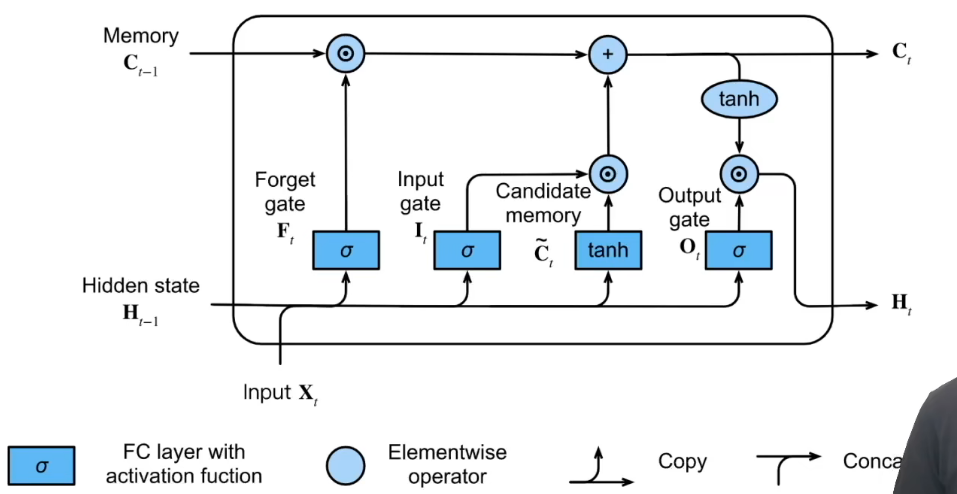
主要关注三个门:
- 忘记门
:将值朝0减少 - 输入门
:决定不是忽略掉输入数据 - 输出门
:决定是不是使用隐状态 - 候选记忆单元
- 记忆元
:控制输入、遗忘、跳过。输入门 控制采用多少来自 的新数据,而遗忘门 控制保留多少过去的记忆元 的内容。 - 隐状态
: ,这就是输出门发挥作用的地方。在长短期记忆网络中,它仅仅是记忆元的 的门控版本。这就确保了 的值始终在区间 内
代码实现:
- 依赖库和初始化模型参数:
1 | import torch |
- 训练:
1 | vocab_size, num_hiddens, device = len(vocab), 256, d2l.try_gpu() |
- 输出:
1 | perplexity 1.1, 22766.8 tokens/sec on cuda:0 |
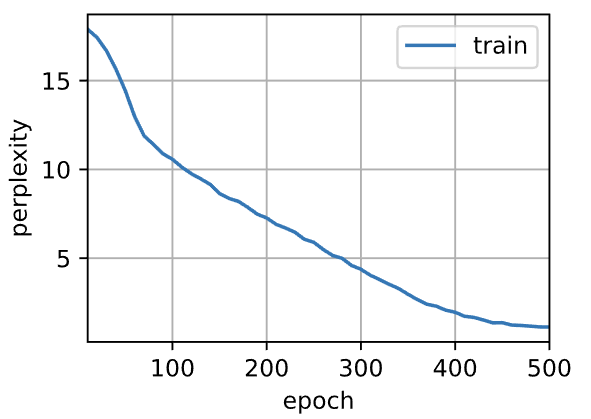
- 利用封装高级API简洁实现:
1 | num_inputs = vocab_size |
1 | perplexity 1.1, 289795.5 tokens/sec on cuda:0 |
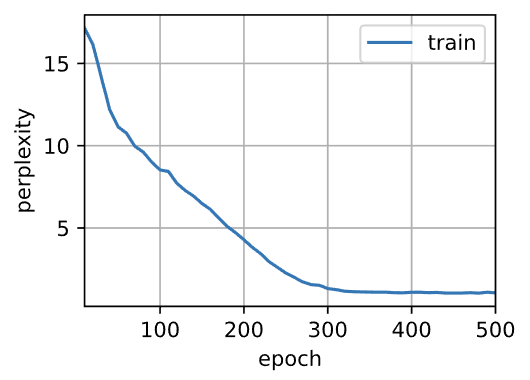
3.3Encoder-Decoder
主要简单复现编码器和解码器的代码架构。
机器翻译是序列转换模型的一个核心问题,其输入和输出都是长度可变的序 列。为了处理这种类型的输入和输出,我们可以设计一个包含两个主要组件的架构:第一个组件是一个编码器 (encoder):它接受一个长度可变的序列作为输入,并将其转换为具有固定形状的编码状态。第二个组件是解码 器(decoder):它将固定形状的编码状态映射到长度可变的序列。这被称为编码器-解码器(encoder‐decoder) 架构
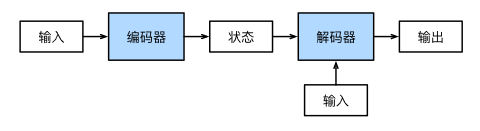
- 编码器:我们只指定长度可变的序列作为编码器的输入X
- 解码器:新增一个
init_state函数,用于将编码器的输出enc_outputs转换为编码后状态。为了逐个生成长度可变的词元序列,解码器在每个时间步都会将输入和编码后的状态映射成当前时间步的输出词元 - 合并结果(编码器-解码器):代码的架构包含了一个编码器和一个解码器,并且可以添加额外的参数。在前向传播中,编码器的输出用于生成编码的状态,这个状态又会被解码器作为其输入的一部分。
1 | from torch import nn |
小结:
- “编码器-解码器”架构可以将长度可变的序列作为输入和输出,因此适用于机器翻译等序列转换问题。
- 编码器将长度可变的序列作为输入,并将其转换为具有固定形状的编码状态。
- 解码器将具有固定形状的编码状态映射为长度可变的序列。
3.4seq2seq
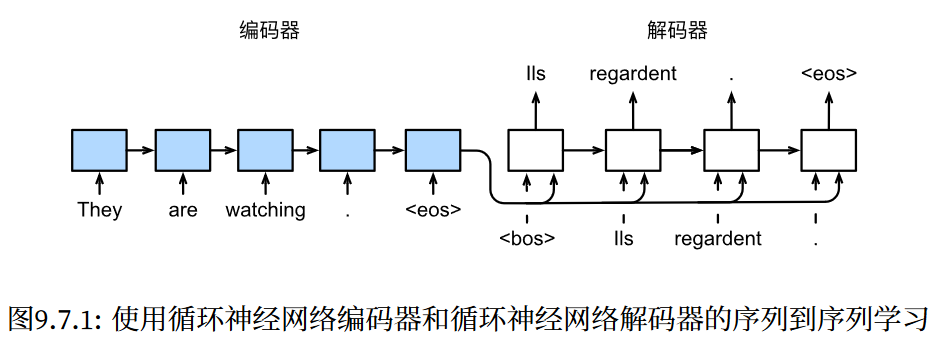
- 导入库
1 | import collections |
- 编码器架构:
1 | class Seq2SeqEncoder(d2l.Encoder): |
实例化上述编码器,最后一层output隐状态输出的一个张量,形状为(时间步数,批量大小,隐藏单元数)state是最后一个时间步的多层隐状态,形状为(隐藏层数量,批量大小,隐藏单元数)
1 | encoder = Seq2SeqEncoder(vocab_size=10, embed_size=8, num_hiddens=16,num_layers=2) |
- 解码器架构:
1 | class Seq2SeqDecoder(d2l.Decoder): |
实例化上述解码器,输出形状为(批量大小,时间步数,词表大小)
1 | decoder = Seq2SeqDecoder(vocab_size=10, embed_size=8, num_hiddens=16, |
- 损失函数:
1 | # 屏蔽不相关项 |
结果就是,第一个序列的损失应为第二个序列的两倍,而第三个序列的损失应为零。
- 训练:
1 | def train_seq2seq(net, data_iter, lr, num_epochs, tgt_vocab, device): |
设置超参数开始训练
1 | embed_size, num_hiddens, num_layers, dropout = 32, 32, 2, 0.1 |
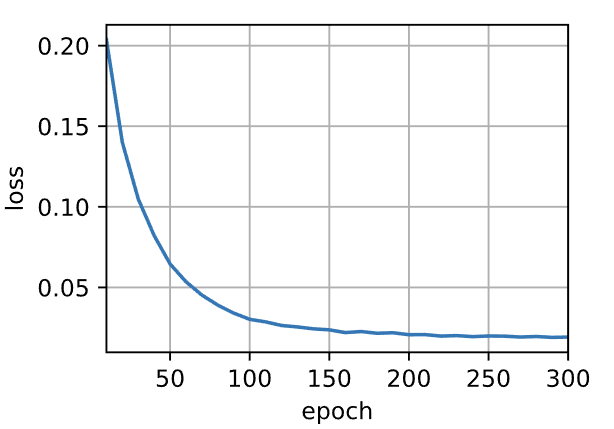
- 定义预测函数以及预测序列评估BLEU:
1 | def predict_seq2seq(net, src_sentence, src_vocab, tgt_vocab, num_steps, |
1 | def bleu(pred_seq, label_seq, k): #@save |
最后利用上述训练好的RNN“编码器-解码器”模型,进行预测并计算BLEU:
1 | engs = ['go .', "i lost .", 'he\'s calm .', 'i\'m home .'] |
输出:
1 | go . => va chercher tom ., bleu 0.000 |
关于seq2seq的思考:
- 根据“编码器-解码器”架构的设计,我们可以使用两个循环神经网络来设计一个序列到序列学习的模型。
- 在实现编码器和解码器时,我们可以使用多层循环神经网络。
- 我们可以使用遮蔽来过滤不相关的计算,例如在计算损失时。
- 在“编码器-解码器”训练中,强制教学方法将原始输出序列(而非预测结果)输入解码器。
- BLEU是一种常用的评估方法,它通过测量预测序列和标签序列之间的
元语法的匹配度来评估预测。
