1.任务
分步构建卷积神经网络并进行部署应用。
2.Convolutional Neural Networks: Step by Step
符号说明:
上标
表示第 层的对象。 - 示例：
是第 层的激活。 和 是第 层的参数。
- 示例：
上标
表示来自第 个示例的对象。 - 示例：
是第 个训练示例输入。
- 示例：
下标
表示向量的第 个条目。 - 示例：
表示第 层激活中的第 个条目，假设这是一个全连接（FC）层。
- 示例：
、 和 分别表示给定层的高度、宽度和通道数。如果你想引用特定的层 ，你也可以写成 、 、 。 、 和 分别表示前一层的高度、宽度和通道数。如果引用特定层 ，这也可以表示为 、 、 。
卷积神经网络的构建块要实现的每个函数的说明步骤：
- 卷积函数，包括：
- 零填充
- 卷积窗口
- 卷积前向传播
- 卷积反向传播（可选）
- 池化函数，包括：
- 池化前向传播
- 创建掩码
- 分配值
- 池化反向传播（可选）
2.1导入库
1 | import numpy as np |
2.2构建网络块
2.2.1Zero-Padding（零填充）
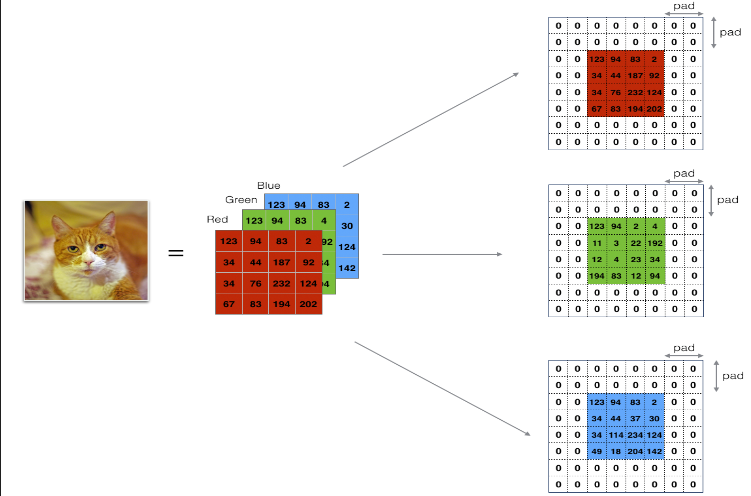
主要好处如下：
它允许你使用卷积层而不必缩小体积的高度和宽度。这对于构建更深的网络非常重要，因为否则在进入更深层次时，高度/宽度会缩小。一个重要的特例是“相同”卷积，在这种卷积中，经过一层处理后，高度/宽度被完全保留。
它帮助我们保留了图像边缘处更多的信息。如果没有填充，图像边缘的像素会对下一层的很少数值产生影响。
代码：
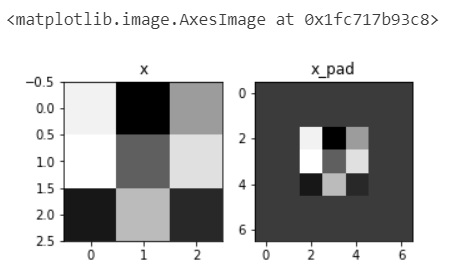
1 | # 评分函数：zero_pad |
部署：
1 | np.random.seed(1) |
输出：
1 | x.shape = (4, 3, 3, 2) |
2.2.2Convolve window（卷积窗口）
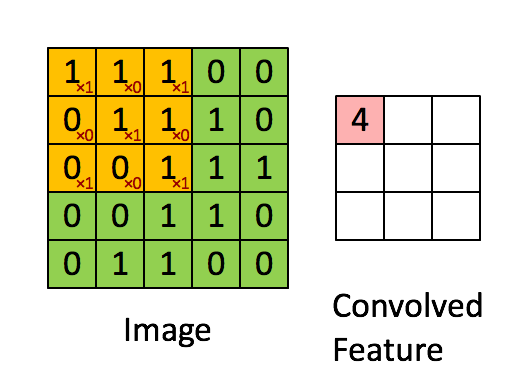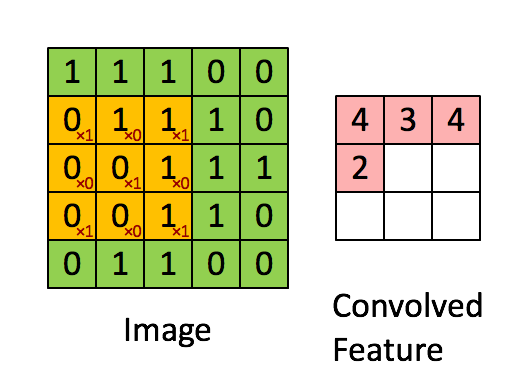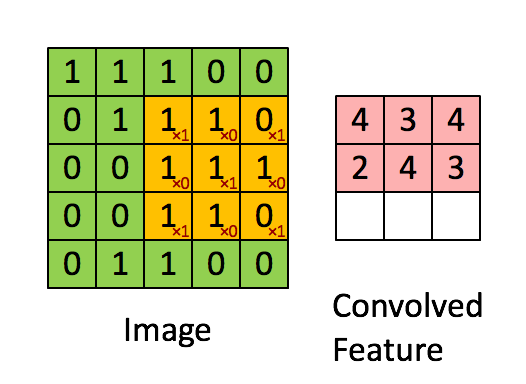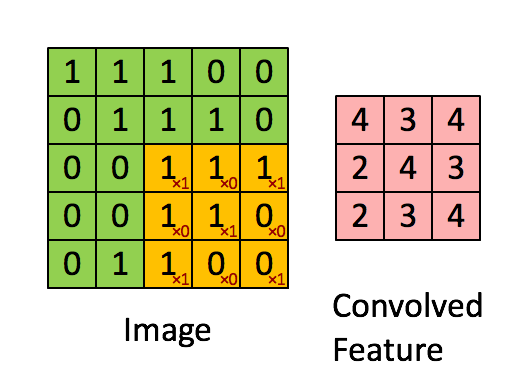
代码：
1 | # 评分函数：conv_single_step |
部署：
1 | np.random.seed(1) |
输出：
1 | Z = -6.999089450680221 |
2.2.3Convolution forward（卷积前向传播）
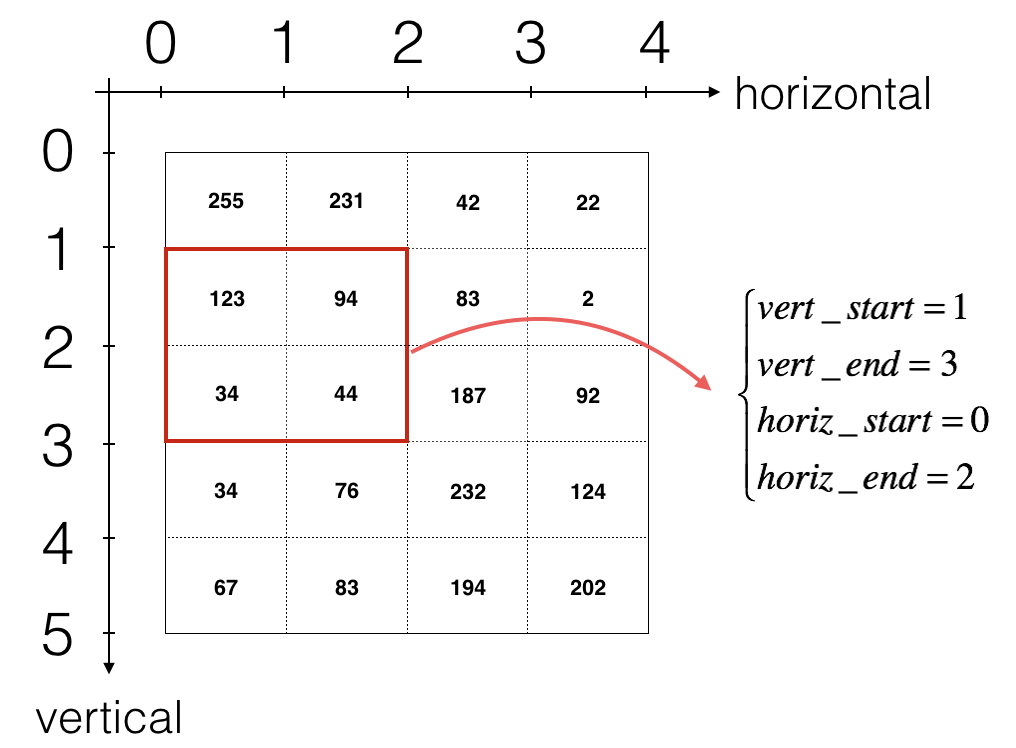
上图只显示单个通道，使用垂直和水平起止（使用 2x2 滤波器）定义切片
卷积的输出形状与输入形状相关的公式是：
$$
\left{
\right.
$$
1 | # 评分函数：conv_forward |
部署：
1 | #生成样例数据 |
输出：
1 | Z's mean = 0.048995203528855794 |
2.2.4Convolution backward（卷积反向传播）
- 计算dA
这是计算相对于某一特定滤波器
$$
dA += \sum {h=0} ^{n_H} \sum{w=0} ^{n_W} W_c \times dZ_{hw} \tag{1}
$$
其中
在代码中，放在适当的 for 循环内，这个公式转化为：
1 | da_prev_pad[vert_start:vert_end, horiz_start:horiz_end, :] += W[:,:,:,c] * dZ[i, h, w, c] |
- 计算dW
这是计算相对于损失的
$$
dW_c += \sum {h=0} ^{n_H} \sum{w=0} ^ {n_W} a_{slice} \times dZ_{hw} \tag{2}
$$
其中
在代码中，放在适当的 for 循环内，这个公式转化为：
1 | dW[:,:,:,c] += a_slice * dZ[i, h, w, c] |
- 计算db
这是计算相对于某一特定滤波器
正如你在基础神经网络中之前所见，
在代码中，放在适当的 for 循环内，这个公式转化为：
1 | db[:,:,:,c] += dZ[i, h, w, c] |
代码：
1 | def conv_backward(dZ, cache): |
部署：
1 | np.random.seed(1) |
输出：
1 | dA_mean = 1.4524377775388075 |
2.2.5Pooling forward（池化前向传播）
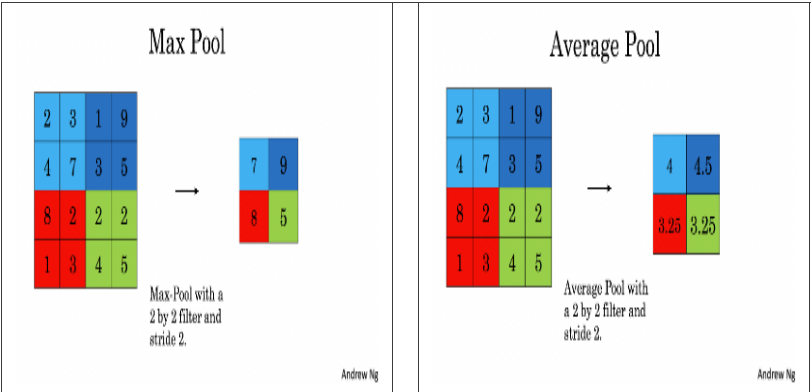
由于没有填充，将池化的输出形状与输入形状绑定的公式是：
$$
\left{
\begin{aligned}
n_H = \lfloor \frac{n_{H_{prev}} - f}{stride} \rfloor +1\
n_W = \lfloor \frac{n_{W_{prev}} - f}{stride} \rfloor +1 \
n_C = n_{C_{prev}}
\end{aligned}
\right.
$$
代码：
1 | # 评分函数：pool_forward |
部署：
1 | np.random.seed(1) |
输出：
1 | mode = max |
2.2.6Pooling backward（池化反向传播）
在跳入池化层的反向传播之前，你将构建一个名为 create_mask_from_window() 的辅助函数，它执行以下操作：
如你所见，这个函数创建了一个“掩码”矩阵，用来追踪矩阵中的最大值位置。真（1）表示 X 中最大值的位置，其它条目为假（0）。你稍后会看到，平均池化的反向传播过程与此类似，但使用的掩码不同。
1.辅助函数代码：
1 | def create_mask_from_window(x): |
部署：
1 | np.random.seed(1) |
输出：
1 | x = [[ 1.62434536 -0.61175641 -0.52817175] |
2.反向传播 backward pass 算法代码：
在最大池化中，对于每个输入窗口，所有对输出的“影响”都来自单个输入值——最大值。在平均池化中，输入窗口的每个元素对输出都有相同的影响。因此，为了实现反向传播，你现在将实现一个反映这一点的辅助函数。
例如，如果我们在前向传播中使用 2x2 滤波器进行平均池化，那么你在反向传播中使用的掩码将看起来像：
这意味着
1 | def distribute_value(dz, shape): |
部署：
1 | a = distribute_value(2, (2,2)) |
输出：
1 | distributed value = [[0.5 0.5] |
- 3.反向传播 Pooling backward 算法代码:
1 | def pool_backward(dA, cache, mode = "max"): |
部署：
1 | np.random.seed(1) |
输出：
1 | mode = max |
