2023-12-2：Hyperparameter tuning and Tensorflow using note

1.任务

学习超参数调试技巧并记录
利用Jupyter Notebook进行Tensorflow的基本操作进行熟悉(X)

2.超参数调试技巧

主要对于这几个超参数进行调试：

：学习率
: momentum（0.9就是一个很好的值）
****：
layers：
hidden units：
learning rate decay：
mini-batch size：保证算法运行有效

2.1随机取值and精确搜索

有粗糙到精细的进行参数的搜索，大概思想如下：

先对这一个范围内的数进行随机均匀取值（合适的步进值）来进行测试，找到效果最好的那个点。

接着聚集于表现效果最好的参数点，对于其周围进行密集取值找到表现最好的点。

这里提到的均匀取值，可以考虑在对数坐标轴上分段进行随机均匀取值（减少计算量和资源占用）

2.2Batch-Normalization

Batch-Normalization是发生在计算z和a之间。

Tensorflow中只需要一行代码：

1	tf.nn.batch-normalization()

2.3Softmax回归

softmax 回归(softmax regression)其实是 logistic 回归的一般形式，logistic 回归用于二分类，而 softmax 回归用于多分类

对于输入数据{(),(),…,()}有个类别，即，那么 softmax 回归主要估算输入数据归属于每一类的概率，即:

上面的式子可以用下图形象化的解析:

Softmax回归代码如下：

def load_dataset(file_path):
    dataMat = []
    labelMat = []
    fr = open(file_path)
    for line in fr.readlines():
        lineArr = line.strip().split()
        dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
        labelMat.append(int(lineArr[2]))
    return dataMat, labelMat


def train(data_arr, label_arr, n_class, iters = 1000, alpha = 0.1, lam = 0.01):
    '''
    @description: softmax 训练函数
    @param {type} 
    @return: theta 参数
    '''    
    n_samples, n_features = data_arr.shape
    n_classes = n_class
    # 随机初始化权重矩阵
    weights = np.random.rand(n_class, n_features)
    # 定义损失结果
    all_loss = list()
    # 计算 one-hot 矩阵
    y_one_hot = one_hot(label_arr, n_samples, n_classes)
    for i in range(iters):
        # 计算 m * k 的分数矩阵
        scores = np.dot(data_arr, weights.T)
        # 计算 softmax 的值
        probs = softmax(scores)
        # 计算损失函数值
        loss = - (1.0 / n_samples) * np.sum(y_one_hot * np.log(probs))
        all_loss.append(loss)
        # 求解梯度
        dw = -(1.0 / n_samples) * np.dot((y_one_hot - probs).T, data_arr) + lam * weights
        dw[:,0] = dw[:,0] - lam * weights[:,0]
        # 更新权重矩阵
        weights  = weights - alpha * dw
    return weights, all_loss
        

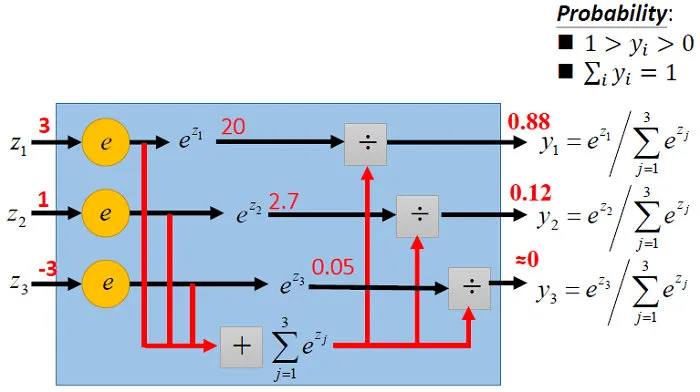
def softmax(scores):
    # 计算总和
    sum_exp = np.sum(np.exp(scores), axis = 1,keepdims = True)
    softmax = np.exp(scores) / sum_exp
    return softmax


def one_hot(label_arr, n_samples, n_classes):
    one_hot = np.zeros((n_samples, n_classes))
    one_hot[np.arange(n_samples), label_arr.T] = 1
    return one_hot


def predict(test_dataset, label_arr, weights):
    scores = np.dot(test_dataset, weights.T)
    probs = softmax(scores)
    return np.argmax(probs, axis=1).reshape((-1,1))


if __name__ == "__main__":
    #gen_dataset()
    data_arr, label_arr = load_dataset('train_dataset.txt')
    data_arr = np.array(data_arr)
    label_arr = np.array(label_arr).reshape((-1,1))
    weights, all_loss = train(data_arr, label_arr, n_class = 4)

    # 计算预测的准确率
    test_data_arr, test_label_arr = load_dataset('test_dataset.txt')
    test_data_arr = np.array(test_data_arr)
    test_label_arr = np.array(test_label_arr).reshape((-1,1))
    n_test_samples = test_data_arr.shape[0]
    y_predict = predict(test_data_arr, test_label_arr, weights)
    accuray = np.sum(y_predict == test_label_arr) / n_test_samples
    print(accuray)

    # 绘制损失函数
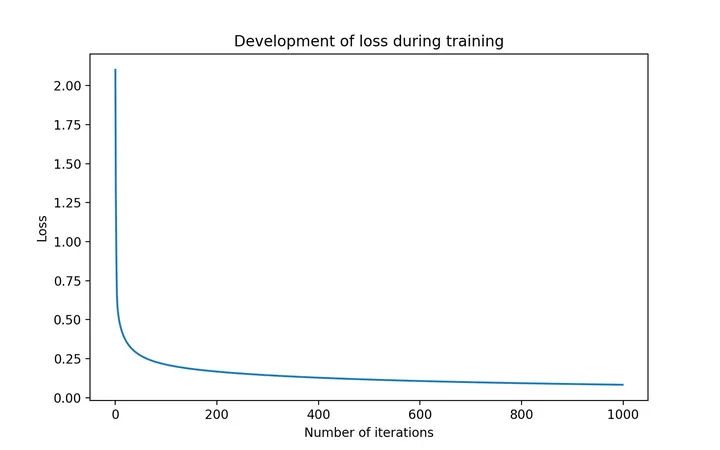
    fig = plt.figure(figsize=(8,5))
    plt.plot(np.arange(1000), all_loss)
    plt.title("Development of loss during training")
    plt.xlabel("Number of iterations")
    plt.ylabel("Loss")
    plt.show()

准确率：

0.9952

详细数据集和代码见此处：https://github.com/HuStanding/ml/tree/master/softmax